2018-12-12

Muffin-tin近似と厳密なポテンシャルとの差について

簡単のため、二個の離れた原子核からのクーロンポテンシャルのみを扱うとする。
この時の、厳密なポテンシャルとMuffin-tin近似との差を見る。

Muffin-tin近似をする際、隣のサイトのポテンシャルの球平均は、以前にまとめた方法を使った。
koideforest.hatenadiary.com

import numpy as np
from matplotlib import pyplot as plt

def norm( x, y, z, x0, y0, z0 ):
    vec = [ x - x0, y - y0, z - z0 ]
    return np.linalg.norm( vec )

def step( x, y, z, x0, y0, z0, rmt ):
    if norm( x, y, z, x0, y0, z0 ) > rmt:
        return 0.
    else:
        return 1.

def site_v( x, y, z, x0, y0, z0 ):
    return - 1. / ( norm( x, y, z, x0, y0, z0 ) + 1e-7 )

def V( x, y, z ):
    xa = 2.
    return site_v( x, y, z, 0, 0, 0 ) + site_v( x, y, z, xa, 0, 0 )

def site_vmt( x, y, z, x0, y0, z0 ):
    R = 2.
    pot_next = - 1. / R
    pot = - 1. / ( norm( x, y, z, x0, y0, z0 ) + 1e-7 ) + pot_next
    return pot

def VMT( x, y, z ):
    xa = 2.
    R = xa
    step1 = step( x, y, z, 0, 0, 0, R/2 )
    step2 = step( x, y, z, xa, 0, 0, R/2 )
    VMT0 = site_vmt( xa/2, 0, 0, 0, 0, 0 ) * ( 1 - step1 ) * ( 1 - step2 )
    pot1 = site_vmt( x, y, z, 0, 0, 0 )  * step1
    pot2 = site_vmt( x, y, z, xa, 0, 0 ) * step2
    return pot1 + pot2 + VMT0

N = 1000
x = np.linspace( -5, 5, N )
y = np.linspace( -5, 5, N )

X, Y = np.meshgrid( x, y )

mat_v   = np.zeros( ( N, N ) )
mat_vmt = np.zeros( ( N, N ) )
for ix, xx in enumerate( x ):
    for iy, yy in enumerate( y ):
        mat_v[ ix ][ iy ] = V( xx, yy, 0 )
        mat_vmt[ ix ][ iy ] = VMT( xx, yy, 0 )

fig = plt.figure( figsize = ( 5, 4 ) )
ax  = fig.add_subplot( 1, 1, 1 )
pcm = ax.pcolormesh( X, Y, mat_v.T, vmin = -3, vmax = 0 )
fig.colorbar( pcm )
plt.show()

fig = plt.figure( figsize = ( 5, 4 ) )
ax  = fig.add_subplot( 1, 1, 1 )
pcm = ax.pcolormesh( X, Y, mat_vmt.T, vmin = -3, vmax = 0 )
fig.colorbar( pcm )
plt.show()

fig = plt.figure( figsize = ( 5, 4 ) )
ax  = fig.add_subplot( 1, 1, 1 )
pcm = ax.pcolormesh( X, Y, mat_v.T - mat_vmt.T, cmap='bwr', vmin = -1.5, vmax = 1.5 )
fig.colorbar( pcm )
plt.show()

f:id:koideforest:20181212011306p:plain — exact

f:id:koideforest:20181212011324p:plain — muffin-tin

f:id:koideforest:20181212011339p:plain — difference

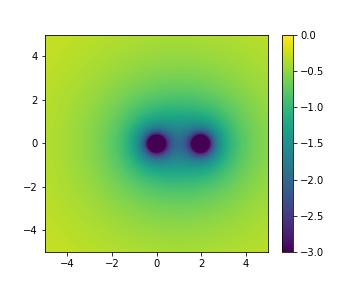
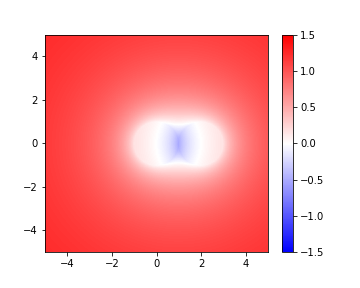
結合方向のある狭い範囲で、ポテンシャルの差が大きいことがわかる。

等高線プロットで参考にしたページ。
[Pythonによる科学・技術計算] 2次元(カラー)等高線等の描画，可視化，matplotlib - Qiita

2018-12-11

誤差関数によるステップ関数でGibbs現象は起こるか？

プログラミング数学

ステップ関数等で不連続に打ち切られた関数をフーリエ変換しようとすると、どんなに頑張っても振動が残る。
これはギブス現象として知られている。
ギブズ現象 - Wikipedia

では、ステップ関数の代わりに誤差関数で滑らかにしたら、どれくらい収束が良いのか？
ちょっと気になったので、やってみた。

まず、誤差関数で作る擬ステップ関数等を定義する。

import numpy as np
from scipy.special import erf
from scipy.integrate import simps
from matplotlib import pyplot as plt

# pseudo step function
def pstep( x, x0, hdx):
    return 0.5 * ( 1 + erf( ( x - x0 ) / ( 0.5 * hdx )  ) )

# pseudo rectangular
def prect( x, L ):
    hdx = L / 16
    return pstep( x, L / 4, hdx ) - pstep( x, 3/4 * L, hdx )

# rectangular
def rect( x, L ):
    func = np.zeros( len( x ) ) 
    for i, xx in enumerate( x ):
        if L / 4 <= xx <= 3/4 * L:
            func[ i ] = 1.0
    return func

滑らかな矩形波をフーリエ変換する。
フーリエ変換はsimpson積分で自前で頑張る。

L = np.pi
N = 120
x = np.linspace( 0, L, N )
k = 2 * np.pi / L * np.arange( -100, 100 + 1 ) 

func  = prect( x, L )
# func = rect( x, L )

fn = []
for kk in k:
    integrand = func * np.exp( -1.j * kk * x )
    fn.append( complex( simps( np.real( integrand ), x ),
                        simps( np.imag( integrand ), x )
                      ) / L
             )

plt.plot( x, func )
fourier = 0.
for i, f in enumerate( fn ):
    fourier += f * np.exp( 1.j * k[ i ] * x )
plt.plot( x, fourier.real )
# fourier.imag is almost zero.

plt.show()

結果

f:id:koideforest:20181211230146p:plain — pseudo rectangular

元の関数をほぼ完全に再現している。
$N = 120$ 程度なので、そんなに大変じゃない。

通常の矩形波に対して同じ条件でやってみた。

f:id:koideforest:20181211230215p:plain — rectangular

収束する気配は無い。
ちなみに $N$ を10倍に増やしても、振動が細かくなるだけで、消えることはない。

滑らかにする大切さを知りました。

2018-12-11

Juliaで一次元井戸型ポテンシャル

プログラミング量子力学

以下のサイトの下の方に、Juliaで一次元のシュレーディンガー方程式を解くPDFが紹介されている。
物理ノートby永井

Juliaの練習としてやってみた。
PDF内では、無限の井戸の中に斥力ポテンシャルを入れた場合をやっているが、ここでは引力ポテンシャルに対してやってみる。
解き方としては、中心差分を用いて二階微分を近似した有限要素法に対応する（と思っている）。
とりあえず、引力ポテンシャルは滅茶苦茶深くした。

using Plots
using LinearAlgebra

function calc_V( N, a, V0 )
    vec_V = zeros( Float64, N )
    center = N * a / 2
    L = N * a / 2
    for i in 1 : N
        x = i * a
        if center - L / 2  <= x <= center + L / 2
            vec_V[ i ] = - V0
        end
    end
    return vec_V
end

function make_H1dv( N, a, V0 )
    mat_H = zeros( Float64, N, N )
    vec_V = calc_V( N, a, V0 )
    for i in 1 : N
        for dx in -1 : 1
            j = i + dx
            v = -1 / ( 2 * a^2 )
            if dx == 0
                v = 1 / a^2 + vec_V[ i ]
            end
            if 1 <= j <= N
                mat_H[ i, j ] = v
            end
        end
    end
    return mat_H
end

function main( N, a, V0 )
    N = 100
    a = 1 / N
    V0 = 1e4
    mat_H = make_H1dv( N, a, V0 )
    energy, phi = eigen( mat_H )
    return energy, phi
end

energy, phi = main()

plot( energy )
savefig( "energy.png" )

plot( phi[ :, 1:5 ] )
savefig( "phi.png" )

f:id:koideforest:20181211191822p:plain — energy

最初の固有値25個くらいは値が負なので、束縛状態であることがわかる。

最初の5個くらいの波動関数を確認すると、

f:id:koideforest:20181211191803p:plain — phi

しっかり中心の有限井戸に束縛されている。

プロットしてみるとわかるが、energyの図の真ん中らへんは、無限井戸も含めた全体に広がる解で、さらに高いエネルギーの解は有限井戸を避けて片側に強く局在した状態になる。
片側だけに寄るのは対称性的におかしいが、そこはまぁ数値解の御愛嬌という感じだろうか。

とりあえず、デカイ箱を用意しておいて、その中に引力ポテンシャルを入れれば、束縛解をパッと出せることがわかった。

2018-12-11

二次元のベクトルの割算について

数学

ベクトルの割算ってなんだ？って思った時に、複素数の割算を考えてみた。

$\displaystyle z = x + i y \\ \displaystyle \frac{ z_2 }{ z_1 } = \frac{ x_2 + i y_2 }{ x_1 + i y_1 } = \frac{ ( x_2 + i y_2 ) ( x_1 - i y_1 ) }{ x_1^2 + y_1^2 } = \frac{ x_1 x_2 + y_1 y_2 }{ | z_1 |^2 } + i \frac{ x_1 y_2 - y_1 x_2 }{ | z_1 |^2 }$

虚数 $i$ は $2 \times 2$ 行列に直すことが出来るので、
$\displaystyle \vec{ v } = ( x, y )^T, \quad E = \pmatrix{ 1 & 0 \\ 0 & 1 } , \quad I = \pmatrix{ 0 & -1 \\ 1 & 0 } \\ \displaystyle \frac{ \vec{ v }_2 }{ \vec{ v }_1 } = E \frac{ \vec{ v }_1 \cdot \vec{ v }_2 }{ v_1^2 } + I \frac{ {\rm det} ( \vec{v_1}, \vec{v_2} ) }{ v_1^2 } \equiv A \\ \therefore \vec{ v }_2 = A \vec{ v }_1$

これはベクトルの変換行列を求めたことに対応する。
$\displaystyle \cos\theta \equiv \frac{ \vec{v}_1 \cdot \vec{v}_2 }{ v_1 v_2 } \\ \displaystyle \sin\theta \equiv \frac{ {\rm det} ( \vec{v_1}, \vec{v_2} ) }{ v_1 v_2 } \\ \displaystyle \cos\theta^2 + \sin\theta^2 = \frac{( x_1^2 x_2^2 + y_1^2 y_2^2 + 2 x_1 x_2 y_1 y_2 ) + ( x_1^2 y_2^2 + x_2^2 y_1^2 - 2 x_1 x_2 y_1 y_2 ) }{ ( x_1^2 + y_1^2 ) ( x_2^2 + y_2^2 ) } = 1$
と定義すれば、回転行列を $v_2 / v_1$ でスケールした変換行列になることがわかる。

$\displaystyle A = E \frac{ v_2 }{ v_1 } \cos\theta + I \frac{ v_2 }{ v_1 } \sin\theta = \frac{ v_2 }{ v_1 } \pmatrix{ \cos\theta & - \sin\theta \\ \sin\theta & \cos\theta }$

ここまで、幾何学的な考察は行っていないが、sineが行列式で表せることが自然と出てきた。
まぁ当たり前と言えば当たり前だが、ちゃんと求まったのは嬉しい。

2018-11-24

単振動をT行列を使って解く。

力学数学

前回、Green関数を使って古典単振動の軌跡を求めた。
koideforest.hatenadiary.com

今回は、無限級数の別表現として、 $T$ 行列を使ってみる。
$T$ 行列は、Green関数を用いて次のように定義出来る。
$\displaystyle \frac{ d^2 }{ d x^2 } x( t ) = f( t ) x( t ), \\ \displaystyle T( t, t' ) = f( t )\delta( t - t' ) + f( t ) G( t, t' ) f( t' ) \\ \displaystyle \quad + \int dt_1 \, f( t ) G( t, t_1 ) f( t_1 ) G( t_1, t' ) f( t' ) + \cdots$

この $T$ 行列を用いて、前回の式を書き直すと、 $f( t ) = -\omega^2$ だから、
$\displaystyle x( t ) = x_0( t ) + \int^\infty_0 dt' \, G( t - t' ) \left( - \omega^2 x_0( t' ) \right) \\ \displaystyle \quad + \int^\infty_0 dt' \int^\infty_0 dt'' \, G( t - t' ) \left( - \omega^2 \right) G( t' - t'' ) \left( - \omega^2 x_0( t'' ) \right) + \cdots \\ \displaystyle \quad = x_0( t ) + \int^\infty_0 dt' \int^\infty_0 dt'' \, G( t - t' ) T( t', t'') x_0( t'' ) \\ \displaystyle T( t', t'' ) = \left( - \omega^2 \right) \delta( t - t' ) + \left( - \omega^2 \right)^2 G( t, t' ) \\ \displaystyle \quad + \left( - \omega^2 \right)^3 \int dt_1 \, G( t, t_1 ) G( t_1, t' ) + \cdots$

ここで、Green関数のインパルス応答としての役割を考えると、作用 $L_t$ 、外力 $F( t )$ に対して、
$\displaystyle L_t x( t ) = F( t ), \quad L_t G( t - t' ) = \delta( t - t' ) \\ \displaystyle x( t ) = x_0( t ) + \int dt' \, G( t - t' ) F( t' )$
と現わせることから、外力を $T$ 行列で表すと、
$\displaystyle F( t' ) = \int dt'' \, T( t', t'' ) x_0( t'' )$
外力を（意味わからんが）「（外力が無い時の）位置に対する応答」としてみなせそうな雰囲気を感じる。

そろそろ実際に $T$ 行列を求めてみる。
Green関数は前回と同様に、以下のものを使用する。
$\displaystyle G( t - t' ) = ( t - t' ) \, \theta( t - t' )$

したがって、
$\displaystyle \int dt_1 \, G( t, t_1 ) G( t_1, t' ) = \theta( t - t' ) \int^t_{t'} dt_1 \, ( t - t_1 ) ( t_1 - t' ) \\ \displaystyle \quad = - \theta( t - t' ) \int^t_{t'} dt_1 \, ( t_1 - t ) ( t_1 - t' ) \\ \displaystyle \quad = - \theta( t - t' ) \int^t_{t'} dt_1 \, \left( ( t_1 - t )^2 + ( t_1 - t ) ( t - t' ) \right) \\ \displaystyle \quad = - \theta( t - t' ) \left( - \frac{ ( t' - t )^3 }{ 3 } + \frac{ ( t' - t )^3 }{ 2 } \right) \\ \displaystyle \quad = \theta( t - t' ) \frac{ ( t - t' )^3 }{ 3! }$
$\theta( t - t' )$ は露わには含まれていないが、 $\theta( t - t_1 ) \theta( t_1 - t' )$ にこの条件が暗に含まれているため、明記化しておく。

以上をまとめると、
$\displaystyle T( t', t'' ) = \left( - \omega^2 \right) \delta( t - t' ) + \left( - \omega^2 \right)^2 \theta( t - t' ) ( t - t' ) \\ \displaystyle \quad + \left( - \omega^2 \right)^3 \theta( t - t' ) \frac{ ( t - t' )^3 }{ 3! } + \cdots \\ \displaystyle \quad = - \omega^2 \left( \delta( t - t' ) - \omega \theta( t - t' ) \sum_{n=0} (-1)^n \frac{ \left( \omega ( t - t' ) \right)^{ 2n+1 } }{ ( 2n+1 )!! } \right) \\ \displaystyle \quad = - \omega^2 \left( \delta( t - t' ) - \omega \theta( t - t' ) \sin \left( \omega ( t - t' ) \right) \right)$

前回の境界条件を引き続き採用すると、 $x_0 = l$ であるから、
$\displaystyle F( t' ) = l \int dt'' \, \left( - \omega^2 \left( \delta( t' - t'' ) - \omega \theta( t' - t'' ) \sin \left( \omega ( t' - t'' ) \right) \right) \right) \\ \displaystyle \quad = - l \omega^2 + l \omega^3 \int^{t'}_0 dt'' \, \sin \left( \omega ( t' - t'' ) \right) \\ \displaystyle \quad = - l \omega^2 \cos \left( \omega t' \right)$

よって、強制振動が外力として加わっているとみなすことが出来る。

無限級数の $T$ 行列による置き換えは、以下のような関係を求めたのと同様であるから、この時点で方程式は解けていると言っても良い。
$\displaystyle - \omega^2 x( t ) = \int dt' T( t, t' ) x_0( t' ) = - l \omega^2 \cos \left( \omega t' \right) \\ \displaystyle \therefore x( t ) = l \cos \left( \omega t \right)$
よって、解が得られた。

もちろん、真面目にGreen関数との積を積分して求めても良い。
$\displaystyle \frac{ x( t ) }{ l } = 1 - \omega^2 \int^\infty_0 dt' \, G( t - t' ) \cos \left( \omega t' \right) = 1 - \omega^2 \int^t_0 dt' \, ( t - t' ) \cos \left( \omega t' \right) \\ \displaystyle \quad = 1 - \omega t \sin \left( \omega t \right) + \left( \omega t \sin \left( \omega t \right) - \omega \int^t_0 dt' \, \sin \left( \omega t' \right) \right) \\ \displaystyle \quad = 1 + \left( \cos \left( \omega t \right) - 1 \right) = \cos \left( \omega t \right) \\ \displaystyle \therefore x( t ) = l \cos \left( \omega t \right)$

計算量は多いが、統一的に扱えるのは理解の助けになると思われる。

2018-11-23

単振動を（非摂動）Green関数を使って解く。

力学数学

前回、Green関数を使って古典力学の基礎問題を解いた。
koideforest.hatenadiary.com
koideforest.hatenadiary.com

今回は古典単振動の軌跡をGreen関数を使って求める。
自由落下の時は、非斉次項が定数だったが、単振動では求めたい関数自身が含まれているため、固有値問題のような形になっている。
そのため、量子力学での摂動展開のような形式で解くため、Green関数のイメージを掴むのにとても良いと思う。

単振動の方程式は以下の通り。
$\displaystyle \frac{ d^2 }{ d x^2 } x( t ) = - \omega^2 x( t ), \\ \displaystyle x( 0 ) = l, \, \dot{ x }( 0 ) = 0, \, t > 0 \quad \left( x( t ) = l \cos( \omega \, t ) \right)$

答えが分かっているので、安心して問題を解き進められる。
Green関数は、境界条件から、自由落下の時と同様のものを使えば良いことがわかる。
$\displaystyle G( t - t' ) = ( t - t' ) \, \theta( t - t' )$

よって、形式的な解は、
$\displaystyle x( t ) = x_0( t ) + \int^\infty_0 dt' \, G( t - t' ) \left( - \omega^2 x( t' ) \right) \\ \displaystyle x_0( t ) = a t + b$

注目するべきは、解くべき $x(t)$ が積分の中で再登場している点である。
量子力学で言えば、リップマン・シュウィンガー方程式と同様の形をしている。
これを解くために、 $x(t')$ に右辺をまるごとそのまま再代入する。
$\displaystyle x( t ) = x_0( t ) + \int^\infty_0 dt' \, G( t - t' ) \left( - \omega^2 x_0( t' ) \right) \\ \displaystyle \quad + \int^\infty_0 dt' \int^\infty_0 dt'' \, G( t - t' ) \left( - \omega^2 \right) G( t' - t'' ) \left( - \omega^2 x( t'' ) \right)$
代入を繰り返すと、無限級数が得られる。

ここで、右辺第二項を計算してみると、
$\displaystyle \int^\infty_0 dt' \, G( t - t' ) \left( - \omega^2 x_0( t' ) \right) = \left( - \omega^2 \right) \int^t_0 dt' \, ( t - t' ) \left( a t' + b \right) \\ \displaystyle = \left( - \omega^2 \right) \left( a \frac{ t^3 }{ 3! } + b \frac{ t^2 }{ 2! } \right)$
よって、少なくとも $t$ の二次以上になる。

境界条件は $x( 0 ), \dot{ x }( 0 )$ で与えられるので、積分を含む項は $t = 0$ で消えてしまい、 $a, b$ の決定に寄与しないことがわかる。
これにより、 $x_0$ に含まれる係数が求まり、 $x_0$ は時間に依存しないことがわかる。
$\displaystyle x( 0 ) = b = l, \, \dot{ x }( 0 ) = a = 0$

これらの結果の整理すると、
$\displaystyle \frac{ x( t ) }{ l } = 1 + \left( - \omega^2 \right) \int^\infty_0 dt' \, G( t - t' ) \\ \displaystyle \quad + \left( - \omega^2 \right)^2 \int^\infty_0 dt' \int^\infty_0 dt'' \, G( t - t' ) G( t' - t'' ) + \cdots$

したがって、問題はGreen関数の積の積分ということになる。
いくつか計算してみる。
$\displaystyle \int^\infty_0 dt' \, G( t - t' ) = \int^t_0 dt' \, ( t - t' ) = \frac{ t^2 }{ 2! } \\ \displaystyle \int^\infty_0 dt' \int^\infty_0 dt'' \, G( t - t' ) G( t' - t'' ) = \int^t_0 dt' \int^{t'}_0 dt'' \, ( t - t' ) ( t' - t'' ) \\ \displaystyle \quad = \int^t_0 dt' \int^{t'}_0 d\tau \, ( t - t' ) \tau = \int^t_0 dt' \, ( t - t' ) \frac{ t'^2 }{ 2! } \\ \displaystyle \quad = \frac{ 1 }{ 2! } \left( \frac{ t^{ 2 + 2 } }{ 2 + 1 } - \frac{ t^{ 2 + 2 } }{ 2 + 2 } \right) = \frac{ 1 }{ 2! } \frac{ t^{ 2 + 2 } }{ ( 2 + 1 )( 2 + 2 ) } = \frac{ t^4 }{ 4! }$

したがって、以下のような一般化が予想できる。
$\displaystyle \quad \int^\infty_0 dt' \, G( t - t' ) \frac{ t'^n }{ n! } = \frac{ 1 }{ n! } \left( \frac{ t^{ n + 2 } }{ n + 1 } - \frac{ t^{ n + 2 } }{ n + 2 } \right) \\ \displaystyle \quad = \frac{ 1 }{ n! } \frac{ t^{ n + 2 } }{ ( n + 1 )( n + 2 ) } = \frac{ t^{n+2} }{ ( n + 2 )! } \\ \displaystyle \therefore \frac{ x( t ) }{ l } = 1 + \left( - \omega^2 \right) \frac{ t^2 }{ 2! } + \left( - \omega^2 \right)^2 \frac{ t^4 }{ 4! } \cdots = \sum_{n=0} ( - 1 )^n \frac{ ( \omega t )^{ 2n } }{ 2n!! } = \cos( \omega t )$

よって、 $x( t ) = l \cos( \omega t )$ と求めることが出来た。

2018-11-23

自由落下をGreen関数で解く。

力学数学

二階微分だけの演算子に対するGreen関数を求めた。
koideforest.hatenadiary.com

求めたと言っても、斉次解が含まれていないので、Green関数の一般解にはなっていない。
斉次解を含めると、

$\displaystyle G_0( t - t' ) = \frac{ | t - t' | }{ 2 } + a t + b$

ここで、自由落下の問題を考える。
$\displaystyle m \frac{ d^2 }{ d t^2 } z( t ) = - m g \rightarrow \frac{ d^2 }{ d t^2 } z( t ) = - g \\ \displaystyle z( 0 ) = 0, \, \dot{ z }( 0 ) = 0, \, t \ge 0$

この時、Green関数を用いると、
$\displaystyle z( t ) = z_0( t ) + \int^{\infty}_0 G_0( t - t' )( - g ) \, dt'$

一応、確認すると、
$\displaystyle \frac{ d^2 }{ d t^2 } z( t ) = \int^{\infty}_0 \frac{ d^2 }{ d t^2 } G_0( t - t' )( - g ) \, dt' = \int^{\infty}_0 \delta( t - t' )( - g ) \, dt' = - g$

Green関数の境界条件を以下のように設定すると、
$\displaystyle G( 0, t' ) = \frac{ t' }{ 2 } + b = 0 \rightarrow b = - \frac{ t' }{ 2 } \\ \displaystyle \frac{ d }{ d t } G( 0, t' ) = \frac{ \theta( - t' ) - \theta( t' ) }{ 2 } + a = - \frac{ 1 }{ 2 } + a \rightarrow a = \frac{ t }{ 2 } \\ \displaystyle \therefore G( t - t' ) = \frac{ | t - t' | }{ 2 } + \frac{ t - t' }{ 2 } = ( t - t' )\theta( t - t' )$
本当にこれで良いのかは知らない。。。
これを用いると、
$\displaystyle z( t ) = z_0( t ) - g \int^{t}_0( t - t' ) \, dt' = z_0( t ) - g \left( t \cdot t - \frac{1}{2} t^2 \right) = z_0( t ) - \frac{ 1 }{ 2 } g t^2$