2017-10-21

分子分母が多項式の関数におけるゼロ近傍の極限

数学量子力学

そもそも分子分母が多項式の時点でやる気がなくなる。すごくやりたくない。苦手意識が強い。
でも多分それは処方箋が頭に入っていないだけ。
今回は対処法を簡単に考察する。

例えば、球ベッセル関数を球ノイマン関数で割ったものにおける原点近傍の振舞が知りたいとする。
それぞれの関数の原点近傍 $\rho \rightarrow 0$ での振舞は、

$j_l( \rho ) \rightarrow \frac{ \rho^l }{ (2l+1)!! } ( 1 - \frac{ \rho^2 }{ 2(2l+3) } + \cdots )$

$n_l( \rho ) \rightarrow - \frac{ (2l+1)!! }{ 2l+1 } \frac{ 1 }{ \rho^{ l+1 } } ( 1 + \frac{ \rho^2 }{ 2(2l-1) } + \cdots )$

こういう多項式同士を割ったものの式をどうやって解すか？というのが今回の焦点。
どこまで多項式の中身を残すかで近似の精度が変わるが、 $\rho \rightarrow 0$ のよくあるパターンとして「0次の次の項まで残す」ことが挙げられる。
最初にこの手のものに出会った時にまず思ったのは、「 $\rho \rightarrow 0$ なんだから多項式の中身は"1"で良くない？」。
こうしなきゃいけないということは基本的にはないはず。でもその慣習みたいなのがあるから、ここで「なんで？」とつまづくと式のグチャグチャ加減から見通しがかなり悪ってしまうと思う。
個人的には、この「一個上も一応入れとく」というノリは、いわゆる有効数字の扱いに近いと思う。あまり重要でないけれど、切り落とし過ぎると気持ち悪い。どこまで正しいのかハッキリしなくて安心出来ない感じ。
多項式の初項だけ残せばもちろん計算は超楽だけど、例えば、それをさらに別の関数に掛けたりした時に一個上の項が効いてくる場合もある。その精神安定剤として「一個残し」は重要だと思う（もちろんどの次数までの近似にしたいかで話は変わってくるが、そういうことがわかる人は多分特に悩んでいないと思う）。

なので、多項式の中身を $\rho^2$ まで残すとする。
安直に割ると、

$\frac{ j_l( \rho ) }{ n_l( \rho ) } \rightarrow - \frac{ 2l+1 }{ ( (2l+1)!! )^2 } \rho^{2l+1} \frac{ 1 - \frac{ \rho^2 }{ 2(2l+3) } }{ 1 + \frac{ \rho^2 }{ 2(2l-1) } }$

ここからどうしようとなるのが、

$\frac{ 1 - \frac{ \rho^2 }{ 2(2l+3) } }{ 1 + \frac{ \rho^2 }{ 2(2l-1) } }$

である。
部分分数分解を用いて、 $1 + \sim$ としても良いが、結局分母をどうするかという問題は残る。この話は後でまた触れる。
ここで、 $\rho \rightarrow 0$ なので、マクローリン展開 $1/(1+x) \sim 1 - x + \dots$ で分母を無くす。

$( 1 - \frac{ \rho^2 }{ 2(2l+3) } )( 1 - \frac{ \rho^2 }{ 2(2l-1) } ) = 1 - \frac{ \rho^2 }{ 2 } ( \frac{ 1 }{ 2l+3 } + \frac{ 1 }{ 2l-1 } ) + O( \rho^4 ) \sim 1 - \rho^2 \frac{ 2l+1 }{ (2l+3)(2l-1) }$

最後のところは $O(\rho^4)$ 、つまり[\rho]の4次の項を無視しただけで、式変形自身はいつも通りである。こんな感じで、多項式の中身としては $j_l, n_l$ と同じオーダーで表すことが出来た。

これを部分分数分解を間に挟むとどうなるか？

$\frac{ 1 - \frac{ \rho^2 }{ 2(2l+3) } }{ 1 + \frac{ \rho^2 }{ 2(2l-1) } } = 1 + \frac{ - \frac{ \rho^2 }{ 2(2l-1) } - \frac{ \rho^2 }{ 2(2l+3) }}{ 1 + \frac{ \rho^2 }{ 2(2l-1) }} = 1 - \rho^2 \frac{ \frac{ 2l+1 }{ (2l+3)(2l-1) } }{ 1 + \frac{ \rho^2 }{ 2(2l-1) }}$

ここでマクローリン展開を使うと同じ解が得られるが、それだったら最初からマクローリン展開を使った方が見通しが良い。問題は、分母に対して $1 + x \rightarrow 1$ $(x \rightarrow 0)$ としてしまっても同じ答えになる点である。それを許してしまうと、最初から分母に $1 + x \rightarrow 1$ の近似をして良いではないか！となり、それによって答えが変わってしまう。
つまり、

$\frac{ 1 - \frac{ \rho^2 }{ 2(2l+3) } }{ 1 + \frac{ \rho^2 }{ 2(2l-1) } } \rightarrow 1 - \frac{ \rho^2 }{ 2(2l+3) }$

にしてしまうと答えが変わる。
そのため、分母に多項式が来て、かつ無限遠ではない有限の点近傍の振舞が知りたい場合には、テイラー展開によって分母を無くすことを考えた方が無難に思える。

2017-10-19

try/except文を用いた欠損データの読み込み

プログラミング

データのフォーマットやらなんやらで、読み込めないデータが混ざっている時、その部分だけをNoneで欠損させて読み込ませたい。
データの区切りが空白" "を場合を想定すると、

f= open( filename, "r" )
lines = f.read().split("\n")
f.close()

for line in lines:

  if not line: continue
  if "\r" in line:
    l = line.strip("\r").split(" ")
  else:
    l = line.split(" ")
  while "" in l: l.remove("")

  data = []
  try:
    data.append( map( float, l ) )
  except:
    ll = []
    for li in l:
      try:
        ll.append( float( li ) )
      except:
        ll.append( None )
    data.append( ll )

最初からmapを使わずに全部のデータを1個ずつfloat出来るかチェックするやり方もあると思うが、何となく泥臭くて嫌だなぁと。
mapで一行丸ごと実数化を試みた後に、上手く行かなかった成分を調べる方が人間に思考に近い気がする。

2017-10-19

テイラー展開、パデ近似をpythonで簡単に表せる日が来た

プログラミング数学

mpmathというモジュールの中にテイラー展開をしてくれmpmath.taylorがいらっしゃる。
Function approximation — mpmath 1.0.0 documentation
mpmath.taylorは展開係数の入ったリストを返してくれる。リストの中身は昇べきの順で並んでいる。

一方、mpmath.polyvalは係数のリストを引数にして多項式の値を返してくれる。
Polynomials — SymPy v0.7.0 documentation
ただし、リストの順番は次数に対して降べきの順である。
したがって、list[::-1]でリストの順番を逆にすればtaylor展開の値がpolyvalですぐに求まる。

#!/usr/bin/env python

import numpy as np
import mpmath as mp
import matplotlib.pyplot as plt

def taylor( f, x, x0, n ):
  coefficients = mp.taylor( f, x0, n)
  return mp.polyval( coefficients[ ::-1], x - x0 )

主要部分はたったこれだけである。
例えばsin関数のマクローリン展開を20乗の項まで展開すると（奇数乗の展開係数はゼロであるため、偶数の次数だけ入力すれば違いを見るのには十分）、

x = np.linspace( 0., 10., 100 )
f = mp.sin
x0 = 0.
for i in range( 10 ):
  plt.plot( x, [ taylor( f, xi, x0, 2 * i ) for xi in x ] ) 
plt.xlim( 0., 10. )
plt.ylim( -5., 5. )
plt.plot( x, [ f( xi ) for xi in x ] )
plt.show()

f:id:koideforest:20171019204501p:plain

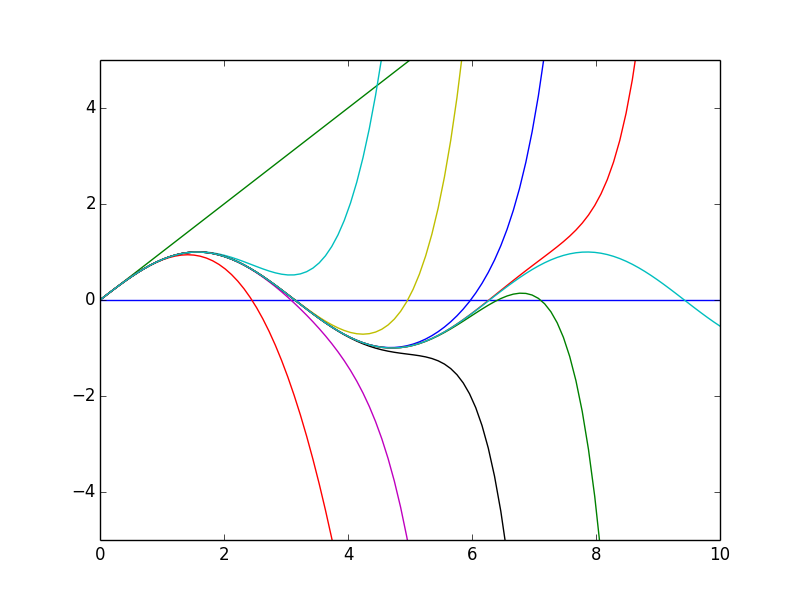
ここでsin関数はmpmathのものでないと動かない。numpy.sinは少なくとも動かなかった。

更に、パデ近似（ペデという人も居るかも）も似たノリで簡単に出来る。
Function approximation — mpmath 1.0.0 documentation
Taylor展開よりも良いと聞かされて来たが、展開係数を求めるのが億劫で、なかなかどんなもんなのか感覚を掴めずにいた。

def pade( f, x, x0, nt, np, nq )
  c_taylor = mp.taylor( f, x0, nt )
  c_p, c_q = mp.pade( c_taylor, np, nq )
  p = mp.polyval( c_p[::-1], x - x0 )
  q = mp.polyval( c_q[::-1], x - x0 )
  return p / q

パデ近似はTaylor展開の次数に合わせて近似を行い、np + nq = ntの制約がかかっている。
とりあえず適当にsin関数を近似してみると、

plt.plot( x, [ taylor( f, xi, x0, 10 ) ], label="taylor" )
plt.plot( x, [ pade( f, xi, x0, 10, 5, 5 ) for xi in x ], label="pade(5,5)" )
plt.plot( x, [ pade( f, xi, x0, 10, 3, 7 ) for xi in x ], label="pade(3,7)" )
plt.plot( x, [ pade( f, xi, x0, 10, 7, 3 ) for xi in x ], label="pade(7,3)" )
plt.plor( x, [ f( xi ) for xi in x ], label="exact" )
plt.legend()
plt.show()

f:id:koideforest:20171019211659p:plain

sin関数だとあまり大きな改善は見られない。
少なくとも、これでいちいち手打ちしなくても近似形が得られるのでだいぶ心がスッキリ。

2017-10-19

化学シフト等、メッシュを変えずにグラフをシフト

プログラミング

グラフをただシフトさせるだけだったら、x軸のデータにシフト量を足し引きすればすぐに出来る。
問題は、例えばシフトさせる前と後で差を取りたい場合に、x軸が揃っていないと差が取れない点である。
つまり、横軸のメッシュは固定したまま、グラフだけ並行移動して欲しいのである。

シフトさせるさせないに関わらず、関数系は変えずにx軸だけ変更したい場合には、関数補間が必要になる。
グラフの形を別の関数でなるべく同じになる様に近似することで、データで与えられていない横軸の点でも値を求められるのである。
自分は大抵の場合には3次のスプライン補間（cubic spline）で大丈夫だと（勝手に）思っている。

これをシフトに応用するのだが、一つ問題がある。
補間には有限区間のデータが必要だが、その区間の外側に関しては基本的には補間は扱えない（補間法にも依るのかも知れないが）。それこそ一部を知って全部を知る逆問題みたいな話になってしまうし、そんなものは多くの境界条件を課さない限り（誤差の範囲でも）一意に決まらない。グラフの関数が完全にわかっているなら、全てのx点に対してy点の値が求まっているのと同義なので、そもそもその場合には補間は必要ない。
そして、シフトさせることによってグラフが補間の範囲からはみ出てしまうのである。
以下、手続きを順を追って説明すると、

$( x_i, y_i ) ( i = 1, 2, 3...)$ のグラフを補間するためのスプライン係数を求める。
これにより、近似関数 $f( x ) ( x_{min} \leq x \leq x_{max} )$ が与えられる。
シフト量を $\Delta$ とし、 $\zeta_i = f( x_i - \Delta )$ を得る。 $\leftarrow$
$( x_i, \zeta_i )$ をプロットすることで、シフトしたグラフを得る。

$\zeta$ を得るところで、 $x_i - \Delta$ が範囲を飛び出してしまい、(python: scipy.interpolate.interp1dでは)エラーが返って来る。
これを回避するためには、あまり格好は良くないが、 $x_i - \Delta$ が範囲を飛び出した時には $\zeta_i = 0$ とするのが一番簡単な方法に思える。

$tan^{-1}(x)$ における横軸のシフトをpythonで実装すると、

#!/usr/bin/env python

import numpy as np
import spicy.interpolate as ipl
import matplotlib.pyplot as plt

x = np.linspace( 0, 10, 11 )
y = np.arctan( x )
f = ipl.interp1d( x, y, kind="cubic" )

shift = 2.
x_shift = [ xxx - shift for xxx in x ]

x_min = x[0]
x_max = x[-1]
y_chemshif = []
for xs in x_shift:
  if x_min <= xs <= x_max:
    y_chemshif.append( f( xs ) )
  else:
    y_chemshif.append( 0. )

plt.plot( x, y, "o", color="red" )
plt.plot( x, y_chemshif, "o", color="blue" )
plt.show()

f:id:koideforest:20171019180617p:plain

2017-10-18

相互作用表示と摂動展開とDyson級数

数学量子力学

q-number（演算子）をハットで表そうとしたらめっちゃズレるので、c-number（演算子じゃない普通の数）は小文字、q-numberは大文字で表すことにする。

$Z = e^{ \alpha ( X + Y ) }$
$O_X ( \alpha ) \equiv e^{ - \alpha X } O e^{ \alpha X }$

とし、

$Z = e^{ \alpha ( X + Y ) } = e^{ \alpha X } F( \alpha )$

と書けるとするならば、 $F( \alpha )$ はどんな形になるか？ということを考える。
多分これを摂動展開と呼んでいる気がする。
ベーカー・ハウスドルフの定理を使えば、

$Z = e^{ \alpha ( X + Y ) } = e^{ \alpha X } e^{ \alpha Y } e^{ - \frac{1}{2} \alpha^2 [ X, Y ] }$
$F( \alpha ) = e^{ \alpha Y } e^{ - \frac{1}{2} \alpha^2 [ X, Y ] }$
追記：この展開は $[ X, Y ]$ が定数の時のみ許される。一般にはこの形は近似形でしかない。ネットに落ちてたこのpdfが丁寧。
http://www2.yukawa.kyoto-u.ac.jp/~akio.tomiya/filebox/Campbell-Baker-Hausdorff.pdf
修正：符号と指数を修正。

と、簡単に求まったように見えるかもしれないが、実際に計算しようとすると指数を級数展開しなきゃいけなかったり、そもそも交換子 $[ X, Y$ ]が求まらないとどうしようもなかったりして、解析的に計算出来る時以外は結構不便。

交換子を出現させずに何か表式が得られるといいなぁというノリで何か方法ないか考える。
それでその取っ掛かりとして $Z$ を $\alpha$ で微分すると、定義から2パターンの形が得られる。

$\frac{ \partial Z }{ \partial \alpha } = ( X + Y ) e^{ \alpha ( X + Y ) } = ( X + Y ) e^{ \alpha X } F( \alpha )$
$\frac{ \partial Z }{ \partial \alpha } = [ \frac{ \partial }{ \partial \alpha } e^{ \alpha X } ] F( \alpha ) + e^{ \alpha X } \frac{ \partial F }{ \partial \alpha } = X e^{ \alpha X } F( \alpha ) + e^{ \alpha X } \frac{ \partial F( \alpha ) } { \partial \alpha }$

したがって、

$Y e^{ \alpha X } F( \alpha ) = e^{ \alpha X } \frac{ \partial F } { \partial \alpha }$
$\frac{ \partial F } { \partial \alpha } = e^{ - \alpha X } Y e^{ \alpha X } F( \alpha ) = Y_X (\alpha) F( \alpha )$

ここまで来ると、相互作用表示でお馴染みの方程式と同じ形になっていることに気づく。

$\frac{ \partial U_I } { \partial ( - i t / \hbar ) } = i \hbar \frac{ d U_I } { dt }= e^{ i H_0 t / \hbar } V e^{ - i H_0 t / \hbar } U_I = V_I U_I$

これを適当な境界条件で積分して逐次代入するとDyson 級数が得られる。

よって、 $H = H_0 + V$ を丸ごと使って時間発展するハイゼンベルグ表示から、 $H_0$ だけで時間発展する部分を抜き出した摂動展開をすると、相互作用表示が与えらえることが直接的に示せた。
つまり、

$U_H (t) = e^{ - i ( H_0 + V ) t / \hbar } = e^{ - i H_0 t / \hbar } U_I (t)$

シュレーディンガー方程式から出発した、相互作用表示の導出に特化した方法がサクライに載っているが、それだと摂動展開とイマイチ繋がらなかったので、スッキリしました。

2017-10-17

yield (generator) の有り難みとは？: python

プログラミング

fortran77及び90・95上がりからすると、昨今のモダンな言語のノリになかなかついて行けないでやんです（バカでごめんなさい）。

そもそもファイルのreadに関して一行ずつ読むのがデフォルトのfotran脳的には、python様がどこでどうメモリを消費しているか、またループが露わに出ていないためどこが律速かわからないのであります。
1GBのファイルを開いてデータを読み込むのを目的とした時に、以下の操作でメモリを食うのか食わんのかがpython様が裏で働き過ぎててわからぬ。

f = open( filename, "w" ) でファイルを開いた時
num_line = sum( 1 for line in open( filename ) ) で行数を数える時
line = f.readline() で一行だけ読んだ時

行数を数えるアルゴリズムは以下から参照
text files - How to get line count cheaply in Python? - Stack Overflow

そりゃあread()やreadlines()でファイルの中身を丸ごと扱おうとしてメモリが足りないとかはわかる。しかしどこで何がどうメモリ使うのかがイマイチわからん。
（「1GBのファイルを用意して自分で一個一個やってどれくらいメモリ食うか自分で調べろよ」という声をここでは盛大に無視することをお許し願いたい。）

こういう思考回路を背景にネット上を徘徊すると、pythonにはyield (generator)という機能があるという事実に出会う。
generatorは以下のサイトが分かり易かった。
ailaby.com

一個一個やるからgeneratorは省メモリですよ〜というノリはわかった。ということは、ファイルを開くだけならばメモリは大して使わないのだろうということは何となく類推出来る。
まさに行数を数えるものを作ろうとする際には、ファイルを丸ごと読み込んでメモリ不足で動かないという事態を起こすことなく安全に処理出来る。
しかし、例えば膨大なデータをプロットしたいとかなった時には、結局全部のデータが必要で、一個一個扱おうがそれをリスト変数なり何なりに格納する場合にはgeneratorの恩恵は無さそうに思える。

自分はビックデータを扱う分野にはまだいないので、何をどうズル工夫してメモリの問題を避けているのかが、イマイチ掴めていない。アルゴリズム等によるメモリ節約の寄与と、メモリを摘みまくったPCの物理的な寄与のどっちが支配的なのかがわからんです。何となく機械学習のプログラムが発達して来たからという風潮を感じつつも、何でもノートPC上で出来る魔法みたいなことは起こってなくて実際は金に物を言わせてる感が否めない。もっと勉強します。

2017-10-14

複素数平面上の漸近とは？

数学量子力学

クーロン散乱の記事を読んでいて、よく考えると???となった位相の問題。
要するに、

$e^{ i ( a + b ) } \rightarrow e^{ i a } \quad ( a \gg b )$ (?)

となるか？というもの。
いや成らんやろ。 $a$ がどんなに大きかろうが、結局 $mod( a, 2\pi )$ が重要なのであって、 $b$ によってもたらされる位相のズレを解消することは出来ない。
一つ有り得る話としては、 $e^{ i b }$ を複素定数として規格化因子に入れてしまうというもの。
$b$ が定数ならそれで良い。しかし例えば、

$e^{ i ( x + {\rm ln}x ) } \rightarrow e^{ i x } \quad ( x \gg {\rm ln}x )$ (?)

というように、変数の依存性が残っているものはどう扱えば良いのだろうか？これは具体的なケースとしては無限遠方において平面波になるかというものである。
数値計算上、適当な境界で一致させるようにその時の $x_0$ で $e^{ i {\rm ln}x_0 }$ を複素定数として抜き出すということは可能だろうが、そうではなく解析的な極限操作、漸近操作において、 $x$ 依存性が残るものをどう捉えられるのだろうか？時計の長針と短針のように、完全に揃い続けることはないものを漸近したと呼んで良いのだろうか？

もう少し勉強してみる必要がありそう。

nano_exit

基礎的なことこそ、簡単な例が必要だと思うのです。

分子分母が多項式の関数におけるゼロ近傍の極限

try/except文を用いた欠損データの読み込み

テイラー展開、パデ近似をpythonで簡単に表せる日が来た

化学シフト等、メッシュを変えずにグラフをシフト

相互作用表示と摂動展開とDyson級数

yield (generator) の有り難みとは？: python

複素数平面上の漸近とは？