ポテンシャルのルジャンドル関数展開

「ポテンシャルの角運動量展開」の二次元版だと思って頂いて差し支えない。

$\displaystyle V( r, \theta ) = \sum_l V_l( r ) P_l( \cos\theta ) \\ \displaystyle V_l( r ) = \frac{ 2 l + 1 }{ 2 } \int^\pi_0 d\theta \, \sin\theta \, P_l( \cos\theta ) V( r, \theta )$

係数 $(2l+1)/2$ はルジャンドル関数の直交関係から出て来る。
koideforest.hatenadiary.com

上記の式を用いて、 $l_{max}=10$ まで展開してみる。

import numpy as np
from math import radians
from scipy.special import legendre
from scipy.integrate import simps
from scipy.interpolate import interp1d, interp2d
from matplotlib import pyplot as plt

def Plx( l, x ):
    # legendre( l ) >>> poly1d([ ... ])
    # poly1d([ ... ])( x ) >>> float
    return legendre( l )( x )

def pw_expand( func, l, r ):
    N = 300
    theta = np.linspace( 0., np.pi, N )
    coeff = ( 2 * l + 1 ) / 2.
    pw = []
    for rr in r:
        integrand = []
        for t in theta:
            x = rr * np.cos( t )
            y = rr * np.sin( t )
            integrand.append( coeff * np.sin( t ) * func( x, y ) * Plx( l, np.cos( t ) ) ) 
        print( np.array( integrand ) )
        pw.append( simps( np.array( integrand ), theta ) )
    return np.array( pw )

# For an interpolated function
def pw_expand_interp( func, l, r ):
    N = 300
    theta = np.linspace( 0., np.pi, N )
    coeff = ( 2 * l + 1 ) / 2.
    pw = []
    for rr in r:
        integrand = []
        for t in theta:
            x = rr * np.cos( t )
            y = rr * np.sin( t )
            integrand.append( coeff * np.sin( t ) * func( x, y )[0] * Plx( l, np.cos( t ) ) ) 
        pw.append( simps( np.array( integrand ), theta ) )
    return np.array( pw )

最初に、真四角の定数ポテンシャルを展開してみる。

N = 500
x = np.linspace( -2, 2, N )
y = np.linspace( -2, 2, N )
X, Y = np.meshgrid( x, y )

mat_v_const = np.zeros( ( N, N ) )
for ix, xx in enumerate( x ):
    for iy, yy in enumerate( y ):
        mat_v_const[ iy ][ ix ] = potential_const( xx, yy )

fig = plt.figure( figsize = ( 5, 4 ) )
ax = fig.add_subplot( 1, 1, 1 )
pcm = plt.pcolormesh( X, Y, mat_v_const, cmap = 'Greys' )
fig.colorbar( pcm )
plt.savefig( "v_const.png" )
plt.show()

f:id:koideforest:20181217080205p:plain — v_const

角運動量は、球対称の時に保存量となるため、球対称に近い時に展開の収束が良いと言える。
これは、フーリエ変換の時に正弦波に近いほど収束が良いのと同じ話である。
そのため、不連続な境界を円周上に持つ真四角ポテンシャルの収束は、最悪だと予想出来る。
実際、全然収束しない。

r = np.linspace( 0, 2 * np.sqrt(2), 200 )
pws = []
for l in range( 10 + 1 ):
    pws.append( pw_expand( potential_const, l, r ) )

r = np.linspace( 0, 2 * np.sqrt(2), 200 )
f_const = [ interp1d( r, pws[ l ], kind = "cubic" ) for l in range( 10 + 1 ) ]
mat_pw_const = np.zeros( ( N, N ) )
l_max = 10
for ix, xx in enumerate( x ):
    for iy, yy in enumerate( y ):
        rr = np.linalg.norm([ xx, yy ])
        tt = np.arctan2( yy, xx )
        for l in range( l_max + 1 ):
            if l % 2 == 0:
                mat_pw_const[ iy ][ ix ] += f_const[l]( rr ) * Plx( l, np.cos( tt ) )

fig = plt.figure( figsize = ( 5, 4 ) )
ax = fig.add_subplot( 1, 1, 1 )
pcm = ax.pcolormesh( X, Y, mat_pw_const, cmap = "bwr", vmin = -1, vmax = 1 )
fig.colorbar( pcm )
plt.savefig( "pw_const_plot.png" )
plt.show()

f:id:koideforest:20181217080304p:plain — pw_const_plot

元のポテンシャルとの差を取ると、展開が上手く行っていない部分がより分かり易くなる。

fig = plt.figure( figsize = ( 5, 4 ) )
ax = fig.add_subplot( 1, 1, 1 )
pcm = plt.pcolormesh( X, Y, mat_pw_const - mat_v_const, cmap = "bwr", vmin = -1, vmax = 1 )
fig.colorbar( pcm )
plt.savefig( "pw_const_plot_diff.png" )
plt.show()

f:id:koideforest:20181217080328p:plain — pw_const_diff_plot

各 $l$ の成分に分解した $V_l( r )$ を見てみると、 $l$ が大きくなっても寄与が消える気配がない。

for ipw, pw in enumerate( pws ):
    plt.plot( r, pw, label = "{:d}".format( ipw ) )
plt.legend()
plt.savefig( "pw_const.png" )
plt.show()

f:id:koideforest:20181217080356p:plain — pw_const

真四角ポテンシャルが隅のパリティ（空間反転に対して対称）を持つため、 $l$ が偶数の時だけ寄与する（ $l$ が奇数の時、パリティは奇）。

次に、境界は球対称だが、中身はランダムポテンシャルで対称性もクソもない場合。（後でポテンシャルを再利用するため、cubic splineで補間して関数として取っておく。）

import random

def potential_random( x, y ):
    if x**2 + y**2 <=1:
        return random.random()
    else:
        return 0.

mat_v_rand = np.zeros( ( N, N ) )
for ix, xx in enumerate( x ):
    for iy, yy in enumerate( y ):
        mat_v_rand[ iy ][ ix ] = potential_random( xx, yy )

f_mat_v = interp2d( x, y, mat_v_rand, kind = "cubic" )
mat_v_interp = np.zeros( ( N, N ) )
for ix, xx in enumerate( x ):
    for iy, yy in enumerate( y ):
        mat_v_interp[ iy ][ ix ] = f_mat_v( xx, yy )

fig = plt.figure( figsize = ( 5, 4 ) )
ax = fig.add_subplot( 1, 1, 1 )
pcm = plt.pcolormesh( X, Y, mat_v_interp, cmap = 'Greys' )
fig.colorbar( pcm )
plt.savefig( "v_rand.png" )
plt.show()

f:id:koideforest:20181217080418p:plain — v_rand

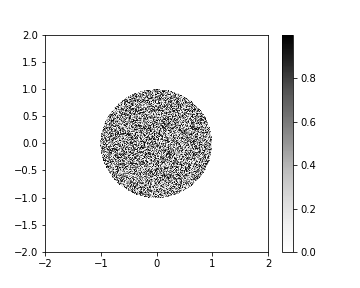
境界が丸いため、その部分は問題が無いが、やはり中身は苦労する。

pws_rand = []
for l in range( 10 + 1 ):
    pws_rand.append( pw_expand_interp( f_mat_v, l, r ) )

f_rand = [ interp1d( r, pws_rand[ l ], kind = "cubic" ) for l in range( 10 + 1 ) ]
mat_rand_pw = np.zeros( ( N, N ) )
l_max = 10
for ix, xx in enumerate( x ):
    for iy, yy in enumerate( y ):
        rr = np.linalg.norm([ xx, yy ])
        tt = np.arctan2( yy, xx )
        for l in range( l_max + 1 ):
            mat_rand_pw[ iy ][ ix ] += f_rand[l]( rr ) * Plx( l, np.cos( tt ) )

fig = plt.figure( figsize = ( 5, 4 ) )
ax = fig.add_subplot( 1, 1, 1 )
pcm = plt.pcolormesh( X, Y, mat_rand_pw, cmap = 'Greys', vmin = 0, vmax = 1 )
fig.colorbar( pcm )
plt.savefig( )
plt.show()

f:id:koideforest:20181217080443p:plain — pw_rand_plot

全然似ても似つかない。
差を取ると、何を再現出来ているのか不明なくらい差が大きい。

fig = plt.figure( figsize = ( 5, 4 ) )
ax = fig.add_subplot( 1, 1, 1 )
pcm = plt.pcolormesh( X, Y, mat_rand_pw - mat_v_interp, cmap = 'bwr', vmin = -1, vmax = 1 )
fig.colorbar( pcm )
plt.show()

f:id:koideforest:20181217080512p:plain — pw_rand_diff_plot

$V_l(r)$ もほぼ全ての $l$ が寄与を持つ。

for ipw, pw in enumerate( pws_rand ):
        plt.plot( r, pw, label = "{:d}".format( ipw ) )
plt.legend( loc = 1 )
plt.savefig( "pw_rand.png" )
plt.show()

f:id:koideforest:20181217080537p:plain — pw_rand

これらは、かなり非現実的なポテンシャルであるため、次回はもう少しマシなポテンシャルを展開してみたいと思う。

nano_exit

基礎的なことこそ、簡単な例が必要だと思うのです。

ポテンシャルのルジャンドル関数展開