2018-09-19

統計的な相関まとめ

数学

平均
$\displaystyle \bar{ x } = \frac{ 1 }{ N } \sum^N_{ i = 1 } x_i$

揺らぎ
$\displaystyle \delta x = x - \bar{ x }$

分散（標準偏差の二乗 or 揺らぎの二乗の平均）
統計学における分散と不偏分散例題でわかりやすく解説 | 全人類がわかる統計学
$\displaystyle s^2 = \overline{ ( \delta x )^2 } = \frac{ 1 }{ N } \sum^N_{ i = 1} ( x_i - \bar{x} )^2 = s_x^2$

標準偏差
 標準偏差 | 統計用語集 | 統計WEB
$\displaystyle s = \sqrt{ \overline{ ( \delta x )^2 } } = \sqrt{ \frac{ 1 }{ N } \sum^N_{ i = 1} ( x_i - \bar{x} )^2 } = s_x$

不偏分散（アンサンブル平均ではない平均で取る）
統計学における分散と不偏分散例題でわかりやすく解説 | 全人類がわかる統計学
$\displaystyle S^2 = \frac{ 1 }{ N - 1 } \sum^N_{ i = 1} ( x_i - \bar{x} )^2$

共分散（分散の一般化）
共分散 | 統計用語集 | 統計WEB
$\displaystyle s_{xy} = \overline{ ( \delta x )\, ( \delta y ) } = \frac{ 1 }{ N } \sum^N_{ i = 1} ( x_i - \bar{x} ) ( y_i - \bar{y} )$

相関係数
 26-3. 相関係数 | 統計学の時間 | 統計WEB
$\displaystyle r_{xy} = \frac{ s_{ xy } }{ s_x s_y }$
スペクトル解析のコヒーレンスの形ほぼそのままであり、コヒーレンスが統計量に強く結びついているのがわかる。
koideforest.hatenadiary.com

偏相関係数（疑似相関が疑われる場合）
26-4. 偏相関係数 | 統計学の時間 | 統計WEB
$\displaystyle r_{xy \cdot z} = \frac{ r_{xy} - r_{ x z } r_{ y z } }{ \sqrt{ 1 - r_{ xz } } \sqrt{ 1 - r_{ yz } } }$
因子 $z$ の条件を除いた時に $x$ と $y$ の間で本当に相関があるのかをチェック出来る（らしい）。

相関係数とは何か。その求め方・公式・使い方と3つの注意点 | アタリマエ！
これらはあくまで直線的な相関を調べることしか出来ない（二次以上の依存関係は極値の場所に依って解析不能）。
また特定の分布を仮定するため、異常なデータに弱い。

2018-09-18

スペクトル解析のコヒーレンスとアンサンブル平均

数学

以前に相関関数をいろいろまとめた。
koideforest.hatenadiary.com
koideforest.hatenadiary.com
koideforest.hatenadiary.com

しかし気になったのは、「今のコヒーレンスの定義では 1 にしかならないのではないか？」という点である。

$\displaystyle s_{fg}( k ) = f^*( k ) g( k ) \\ \displaystyle s_f( k ) = \left| f( k ) \right|^2, \qquad s_g( k ) = \left| g( k ) \right|^2 \\ \displaystyle {\rm coh}^2_{fg}( k ) = \frac{ \left| s_{fg}( k ) \right|^2 }{ s_f( k ) s_g( k ) } = \frac{ ( f^*( k ) g( k ) ) ( f( k ) g^*( k ) ) }{ \left| f( k ) \right|^2 \left| g( k ) \right|^2 } = 1$

広島大の講義ノートにクロススペクトルの意味についての記述を見つけた。
https://home.hiroshima-u.ac.jp/nishino/Classforundergraduate/Keisoku/keisoku2shou.pdf
しかし、フーリエ変換しているのになぜか変換前の引数に依存しているし、百歩譲ってそれは良しとしても、平面波から勝手に $\cos$ 関数が出て来ているし、意味不明である。

ポイントは、アンサンブル平均にある。
何回か同じ測定をして、データのセットが $N$ 個あるとすると、
$\displaystyle \bar{ x } \equiv \frac{ 1 }{ N } \sum^N_{ i = 1 } x_i$

簡単のため、今 $N=2$ として各スペクトルのアンサンブル平均を求めると、
$\displaystyle \bar{ s }_f( k ) = \frac{ | f_1( k ) |^2 + | f_2( k ) |^2 }{2}, \qquad \bar{ s }_f( k ) = \frac{ | f_1( k ) |^2 + | f_2( k ) |^2 }{2} \\ \displaystyle \bar{ s }_{fg}( k ) = \frac{ f^*_1( k ) g_1( k ) + f^*_2( k ) g_2( k ) }{ 2 }$

これらを用いてコヒーレンスを計算すれば、
$\displaystyle {\rm coh}^2_{fg}( k ) = \frac{ \left| \bar{ s }_{fg}( k ) \right|^2 }{ \bar{ s }_f( k ) \bar{ s }_g( k ) } = \frac{ | f_1 |^2 | g_1 |^2 + f^*_1 f_2 g_1 g^*_2 + f_1 f^*_2 g^*_1 g_2 + | f_2 |^2 | g_2 |^2 }{ | f_1 |^2 | g_1 |^2 + | f_1 |^2 | g_2 |^2 + | f_2 |^2 | g_1 |^2 + | f_2 |^2 | g_2 |^2 } \\ \displaystyle = \frac{ | f_1 |^2 | g_1 |^2 + 2 \Re \left( f^*_1 f_2 g_1 g^*_2 \right) + | f_2 |^2 | g_2 |^2 }{ | f_1 |^2 | g_1 |^2 + | f_1 |^2 | g_2 |^2 + | f_2 |^2 | g_1 |^2 + | f_2 |^2 | g_2 |^2 }$

これで分母と分子に違いが出た。クロススペクトルによって、データセット間の $f$ もしくは $g$ 同士の関係を考慮することが出来る。

したがって、このコヒーレンスはそもそも統計量に関するものであり、「入力と出力の波形がどれくらい似ているか」ではなく、「複数回測定しても強く再現される信号はどの波数成分か」を表すものと言える。（その意味で「相関」と言えなくもないが、相関関数の相関とは別な意味だと思う）
そのため、全てのデータセットが全く同じものの場合（もしくは一度しか測定を行わなかった場合）、コヒーレンスは常に 1 になる。

2018-09-18

三角関数の相関関数

数学

以前の記事で、相関関数、及びそのガウス関数の時の振舞について調べた。
koideforest.hatenadiary.com
koideforest.hatenadiary.com

ここでは三角関数（ $\cos kx$ ）を使って相関関数の振舞を調べる。

フーリエ変換の定義
$\displaystyle f(k) = \int f(x) e^{ - i k x } dx, \qquad f(k) = \frac{ 1 }{ 2 \pi } \int f(k) e^{ i k x } dk$

三角関数（ $\cos kx$ ）
$\displaystyle f( x ) = \cos( k_0 x ) \rightarrow f( k ) = \pi ( \delta( k - k_0 ) + \delta( k + k_0 ) )$

自己相関関数の定義
$\displaystyle h_f( \xi ) = \int f( x ) f( x + \xi ) dx = \frac{ 1 }{ 2 \pi } \int s_f( k ) e^{ i k \xi } dk, \qquad s_f( k ) = \left| f( k ) \right|^2$

スペクトルと自己相関関数
$\displaystyle s_f( k ) = \pi^2 \delta( 0 ) ( \delta( k - k_0 ) + \delta( k + k_0 ) ) = \pi \delta( 0 ) f( k ) \\ \displaystyle \qquad \rightarrow h( \xi ) = \pi \delta( 0 ) \cos( k_0 \xi )$
デルタ関数の二乗は以下のサイトを参照。
やっと「δ関数の２乗」：T_NAKAの阿房ブログ
無限空間の積分なので、自己相関は発散します。

相互相関関数の定義
$\displaystyle h_{fg}( \xi ) = \int f( x ) g( x + \xi ) dx = \frac{ 1 }{ 2 \pi } \int s_{fg}( k ) e^{ i k \xi } dk, \qquad s_{fg}( k ) = f^*( k ) g( k )$

三角関数
$\displaystyle f( x ) = \cos( k_0 x ) \rightarrow f( k ) = \pi ( \delta( k - k_0 ) + \delta( k + k_0 ) ) \\ \displaystyle g( x ) = \cos( k_0 ( x - x_1 ) \rightarrow g( k ) = \pi ( \delta( k - k_0 ) + \delta( k + k_0 ) ) e^{ i k x_1 }$

クロススペクトルと相互相関関数
$\displaystyle s_{fg}( k ) = \pi^2 \delta( 0 ) ( \delta( k - k_0 ) + \delta( k + k_0 ) ) e^{ i k x_1 } = \pi \delta( 0 ) g( k ) \\ \displaystyle \qquad \rightarrow h_{fg}( \xi ) = \pi \delta( 0 ) \cos( k_0 ( \xi + x_1 ) )$

コヒーレンスと位相
$\displaystyle {\rm coh}^2_{fg}( k ) = \frac{ \left| s_{fg}( k ) \right|^2 }{ s_{f}( k ) s_{g}( k ) } = 1 \\ \displaystyle \theta_{fg}( k ) = \frac{ \Im s_{fg} }{ \Re s_{fg } } = k x_1$
やはりズラした程度ではコヒーレンスは破れず、一方で位相は並行移動の情報を含んでいる。

追記：
コヒーレンスについて再考
koideforest.hatenadiary.com

2018-09-18

ガウス関数の相関関数

数学

以前の記事で相関関数をまとめた。
koideforest.hatenadiary.com
ここではガウス関数を使って、振舞を調べる。

フーリエ変換の定義
$\displaystyle f( k ) = \int f( x ) e^{ - i k x } dx, \qquad f( x ) = \frac{ 1 }{ 2 \pi } \int f( k ) e^{ i k x } dx$

自己相関関数
$\displaystyle h_f( \xi ) = \int f( x ) f( x + \xi ) d\xi = \frac{1}{2\pi} \int \left| f( k ) \right|^2 e^{ i k \xi } dk = \frac{1}{2\pi} \int s_f( k ) e^{ i k \xi } dk$

ガウス関数
$\displaystyle f( x ) = e^{ - a x^2 } \rightarrow f( k ) = \sqrt{ \frac{ \pi }{ a } } e^{ - \frac{ k^2 }{ 4 a } }$

$\displaystyle f( k ) = e^{ - b k^2 } \rightarrow f( x ) = \frac{ 1 }{ \sqrt{ 4 \pi b } } e^{ - \frac{ x^2 }{ 4 b } }$

スペクトルと自己相関関数
$\displaystyle s_f( k ) = \left| f( k ) \right|^2 = \frac{ \pi }{ a } e^{ - \frac{ k^2 }{ 2 a } } \rightarrow h_f( \xi ) = \sqrt{ \frac{ \pi }{ 2 a } } e^{ - \frac{ a }{ 2 } \xi^2 }$
$\xi = 0$ で、 $h( 0 ) = \sqrt{ \pi / 2 a }$ がちゃんと求まっていることがわかる。

相互相関関数の定義
$\displaystyle h_{fg}( \xi ) = \int f( x ) g( x + \xi ) d\xi = \frac{1}{2\pi} \int f^*( k ) g( k ) e^{ i k \xi } dk = \frac{1}{2\pi} \int s_{fg}( k ) e^{ i k \xi } dk$

より一般的なガウス関数
$\displaystyle f( x ) = e^{ - a_f ( x - x_f )^2 } \rightarrow f( k ) = \sqrt{ \frac{ \pi }{ a_f } } e^{ i k x_f } e^{ - \frac{ k^2 }{ 4 a_f } } \\ \displaystyle g( x ) = e^{ - a_g ( x - x_g )^2 } \rightarrow g( k ) = \sqrt{ \frac{ \pi }{ a_g } } e^{ i k x_g } e^{ - \frac{ k^2 }{ 4 a_g } }$

クロススペクトルと相互相関関数
$\displaystyle s_{fg}( k ) = f^*( k ) g( k ) = \frac{ \pi }{ \sqrt{ a_f a_g } } e^{ i k ( x_f - x_g ) } e^{ - \frac{ a_f + a_g }{ 4 a_f a_g } k^2 } \\ \displaystyle \qquad \rightarrow h_{fg}( \xi ) = \sqrt{ \frac{ \pi }{ a_f + a_g } } e^{ - \frac{ a_f a_g }{ a_f + a_g } ( x - ( x_f - x_g ) )^2 }$

コヒーレンスと位相
$\displaystyle {\rm coh}^2_{fg}( k ) = \frac{ \left| s_{fg} \right|^2 }{ s_f s_g } = 1 \\ \displaystyle \theta_{fg} = \tan^{-1}\frac{ \Im s_{fg}( k ) }{ \Re s_{fg}( k ) } = - k( x_f - x_g )$
~~関数を並行移動させた程度では、コヒーレンスは（最大値のまま）変わらないため、本質的な関数の形の議論に役立ちそう。~~
以下で追加考察。
koideforest.hatenadiary.com

一方で、位相は関数の並行移動をもろに受ける。波数に対して位相が線形ならば、関数が単に並行移動していると言えそう。

2018-09-16

ガウス関数のフーリエ変換 (scipy.fftpack)

プログラミング数学

ガウス関数はフーリエ変換しても、数式上は（幅は変わるが）またガウス関数になる。
高速フーリエ変換（FFT）とフーリエ変換との関係を以前まとめたため、FFTを用いてガウス関数をフーリエ変換する。
koideforest.hatenadiary.com

ここではscipy.fftpackを用いてFFTを行うが、（少なくともこの場合）出力される配列データの並びが「（正の振動数のデータ）、（負の振動数のデータ）」となっており、そのままプロットするとガウス関数に見えない。

試しにやってみる。

import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft

a = 1
f = lambda x: np.exp( - a * x**2 )  # Gauss function

max_x  = 10.
min_x  = -10.
N      = 2**7
x = np.linspace( min_x, max_x, N )
data   = f( x )
delta_x  = x[1] - x[0]  # ( max_x - min_x ) / ( N - 1 )

# Fast Fourier Transformation 
tilde_f = fft( data ) * delta_x

delta_k = 1. / delta_x / ( N - 1 )
k = np.arange( 0, 1./delta_x + delta_k, delta_k ) * 2. * np.pi

plt.plot( k,  abs( tilde_f ), "o" )
plt.show()

f:id:koideforest:20180916224622p:plain

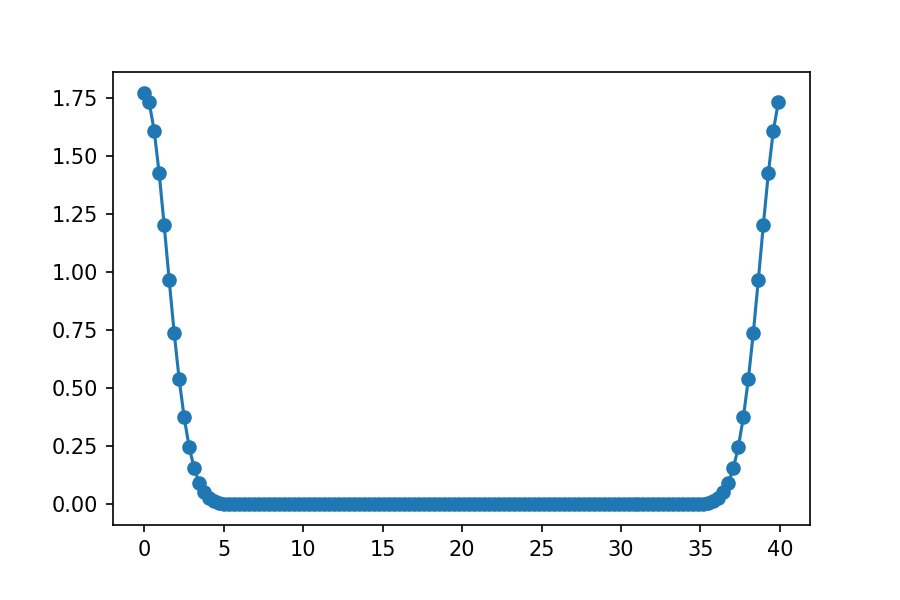
データの並びに関しては、以下のサイトが参考になる。
fft - memoring
SciPy FFTpack
Fourier Transforms (scipy.fftpack) — SciPy v1.1.0 Reference Guide

もう少し説明すると、FFTにおけるアルゴリズムの性質上、fft で生成した配列は、直感的な[ -N/2, ..., N/2 ]という順番では無く、

[ 0, 1, ,2, ... (N/2 - 1), N/2, -N/2, (-N/2 + 1), ..., -1 ]

という風になっている。
つまり、

[ （正の振動数：昇順）、（負の振動：降順）]

である。

fftpackに内蔵されている fftfreq を使うと、fft と同様な並びの横軸を作成してくれる。

from scipy.fftpack import fftfreq 

freq = fftfreq( N, delta_x ) * 2. * np.pi

plt.plot( freq, abs( tilde_f ), "-o" )
plt.show()

f:id:koideforest:20180916224702p:plain

点でプロットするならば問題無いが、線を追加すると N/2 → -N/2 に移るときの線が現れてしまう。
そこで、配列の並びを直感的に戻してくれる関数 fftshift が用意されている。

from scipy.fftpack import fftshift

tilde_f_shift = fftshift( tilde_f )
freq_shift = fftshift( freq )

gauss_k = lambda k: np.sqrt( np.pi / a ) * np.exp( - k**2 / ( 4. * a ) )

plt.plot( freq_shift, abs( tilde_f_shift ), "-o" )
put.plot( freq_shift, gauss_k( freq_shift ), "x" )
plt.show()

f:id:koideforest:20180916224802p:plain
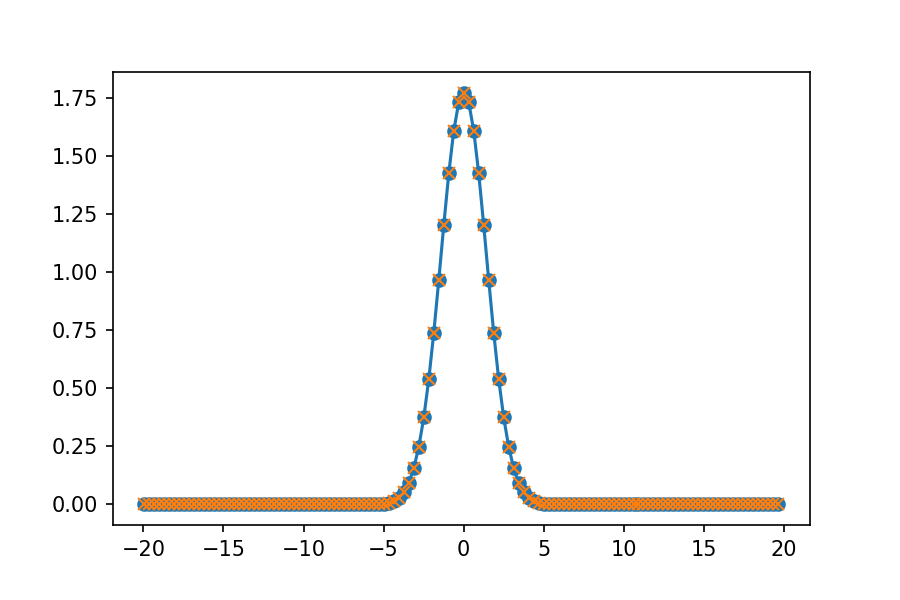
解析的に求めた解も一緒にプロットした。
$\displaystyle f( x ) = e^{ - a x^2 } \\ \displaystyle f( k ) = \sqrt{ \frac{ \pi }{ a } } e^{ - \frac{ k^2 }{ 4 a }}$

解析解の導出は以下のサイトが分かり易い。ただし、指数の係数 $a$ は省略されている。
ガウス関数のフーリエ変換 | ポップラーン

しかし、FFTを用いたガウス関数のフーリエ変換で最も問題なのは、実は数値解が振動している点である。
虚部は実部に比べて小さいため、実部のみプロットすると、

plt.plot( freq_shift, tilde_f_shift.real, "-o" )
plt.plot( freq_shift, abs( tilde_f_shift ), "-" )
plt.show()

f:id:koideforest:20180916230025p:plain

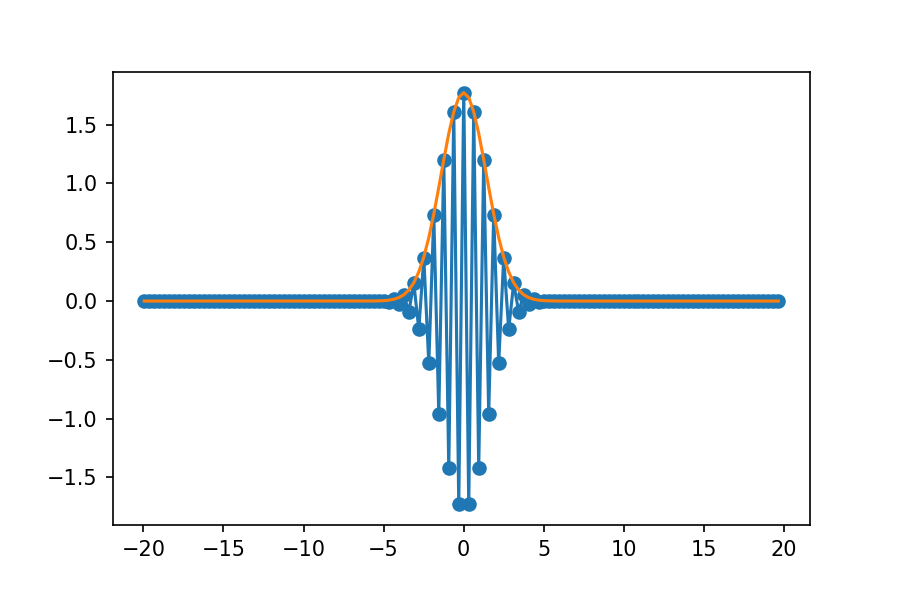
何故、振動が現れるのかは、今の所パッと思い付かないが、フーリエ変換はなかなか侮れないことを教えてくれていると思う。

2018-09-16

高速フーリエ変換（FFT）を使ってフーリエ変換する方法

数学

高速フーリエ変換（FFT）は結局は離散フーリエ変換であり、どちらかというとフーリエ級数展開に近い。
高速フーリエ変換 - Wikipedia

FFTは結局は級数展開、つまり「和」なので、フーリエ変換、つまり「積分」にするためには、変換が必要である。
http://hooktail.sub.jp/mathInPhys/riemannIntegra/

多くの場合には、フーリエ変換は信号解析で用いられるため、時間 $t$ と振動数 $f$ を変数に用いることが多い。
ここでは信号データを $s( t )$ 、そのフーリエ成分を $S( f )$ として考える。

データ数が $N$ の時のFFTの式：
$\displaystyle S( f ) = \sum^{ N - 1 }_{ j = 0 } s( t_j ) e^{ - i 2 \pi f \frac{ j }{ N } } \\ \displaystyle s( t ) = \frac{ 1 }{ N } \sum^{ N - 1 }_{ j = 0 } S( f_j ) e^{ i 2 \pi t \frac{ j }{ N } }$
少なくともpythonのscipy.fftpackではこの定義に従っていると思われるため、横軸は振動数 $f$ で出力される。

これをフーリエ変換を見比べる。以下では $\omega = 2 \pi f$ を使い、 $\omega$ に変数変換した後のフーリエ成分を $\bar{S}(\omega)$ とすると。
$\displaystyle \bar{S}( \omega ) = \int^{ \infty }_{ -\infty } s( t ) e^{ - i \omega t } \, dt \\ \displaystyle s( t ) = \frac{ 1 }{ 2 \pi } \int^{ \infty }_{ -\infty } \bar{S}( \omega ) e^{ i \omega t }$

「和」を「積分」に変換するには、積分における「 $dt$ 」に対応するものが必要である。それがなければ、いくらデータ間隔を細かくしたところで積分にはならない。
データ間隔 $\Delta_t( N )$ を以下のように定義する。
$\displaystyle \Delta_t( N ) = t_{ j + 1 } - t_j = ( t_{ N-1 } - t_0 ) / ( N - 1 ) \equiv T / ( N - 1 )$

これを用いて、和を積分に変換する。
$\displaystyle S( f ) = \sum^{ N - 1 }_{ j = 0 } s( t_j ) e^{ - i 2 \pi f \frac{ j }{ N } } = \frac{ 1 }{ \Delta_t( N ) } \sum^{ N - 1 }_{ j = 0 } s( t_j ) e^{ - i 2 \pi f \frac{ j }{ N } } \Delta_t( N ) \\ \displaystyle \qquad \rightarrow \lim_{N \rightarrow \infty} \frac{ 1 }{ \Delta_t( N ) } \sum^{ N - 1 }_{ j = 0 } s( t_j ) e^{ - i 2 \pi f \frac{ j }{ N } } \Delta_t( N ) \\ \displaystyle \qquad = \lim_{N \rightarrow \infty} \frac{ 1 }{ \Delta_t( N ) } \int^{ \infty }_{ -\infty } s( t ) e^{ - i 2 \pi f t } \, dt \\ \displaystyle \qquad = \lim_{N \rightarrow \infty} \frac{ 1 }{ \Delta_t( N ) } \bar{S}( \omega ) = \lim_{N \rightarrow \infty} \frac{ 1 }{ \Delta_t( N ) } \bar{S}( 2 \pi f )$

したがって、十分大きい $N$ を用いたとき、近似的に以下の関係が成り立つ。
$\displaystyle \bar{S}( \omega ) \sim \Delta_t( N ) S( f ) = \Delta_t( N ) S( \omega / 2 \pi )$
数式上では、 $\omega$ を用いることが（少なくとも自分の分野では）多いため、 $f$ か $\omega$ に揃えておかないと混乱する。

フーリエ変換した $\bar{S}(\omega)$ にフィルターを掛けた後に逆変換をしたい場合には、対応する $S(\omega/2\pi)$ をFFTで逆変換すれば良い。

2018-09-15

古典的な相関関数のまとめ

数学

「相関とは内積の拡張のようなものである」という説明で納得した。
相関関数 [物理のかぎしっぽ]

離散的な数直線上の点 $x_1, x_2, \cdots$ における関数値 $( f(x_1), f(x_2), \cdots )$ をベクトル $\vec{f}$ と思えば、内積 $h$ は

$\displaystyle h = \vec{ f } \cdot \vec{ g } = \sum_i f( x_i ) g( x_i )$

と表せる。これがゼロのとき、関数 $f, \, g$ は互いに直交していると言える。

ここで、 $x$ を連続量に置き換え、それに伴って和を積分に置き換えれば、内積を拡張したものが得られる。

$\displaystyle h = \int f( x ) \, g( x ) \, dx$

これを相関と呼ぶ。
$f = g$ もしくは $f \neq g$ のときをそれぞれ自己相関、相互相関と呼ぶ。
自己相関は、ベクトルで言えば「ノルムの二乗」に相当する。
自己相関がゼロで無いときに、相互相関がゼロになる場合、互いに直交すると言える。

フーリエ変換も、ある波数の平面波との相関を取ったものである。
$\displaystyle f( k ) = \int^{\infty}_{-\infty} f( x ) \, e^{ - i k x } \, dx, \\ \displaystyle f( x ) = \frac{ 1 }{ 2 \pi } \int^{\infty}_{-\infty} f( k ) \, e^{ i k x } \, dk$

しかし、自己相関関数と言うと、意味が変わる。
http://www.jspf.or.jp/Journal/PDF_JSPF/jspf2009_09/jspf2009_09-620.pdf
自己相関関数は、自分自身をズラしたものとの相関であり、ズラす量を引数に持つ。
$\displaystyle h( \xi ) = \int f( x ) \, f( x + \xi ) \, dx$

$h(\xi)$ を $h(0)$ 、つまり、自己相関で規格化したものを自己相関係数と呼ぶ。

$\displaystyle c( \xi ) = h(\xi) / h(0), \qquad c( 0 ) = 1$

関数 $f(x)$ が周期的な場合、自己相関関数（係数）も周期的に振動し、 $c$ が最初に $x$ を跨ぐ $\xi_0$ は変動の速さを特徴付ける量として使うことが出来る。

自己相関関数の被積分関数をフーリエ変換を用いて表すと、
（ただし、 $f(x)$ は実関数で積分区間外でゼロ（ $f(x) = 0 \, ( x < a, b < x)$ ））
$\displaystyle h_f( \xi ) = \int^b_a f( x ) \, \left( \frac{ 1 }{ 2 \pi } \int^{\infty}_{-\infty} f( k ) e^{ i k ( x + \xi ) } \, dk \right) \, dx, \\ \displaystyle \qquad = \frac{ 1 }{ 2 \pi } \int^{\infty}_{-\infty} \left( \int^b_a f( x ) e^{ i k x }\, dx \right) \, f( k ) e^{ i k \xi } \, dk, \\ \displaystyle \qquad = \frac{ 1 }{ 2 \pi } \int^{\infty}_{-\infty} \left( \int^{\infty}_{-\infty} f( x ) e^{ - i k x }\, dx \right)^* \, f( k ) e^{ i k \xi } \, dk, \\ \displaystyle \qquad = \frac{ 1 }{ 2 \pi } \int^{\infty}_{-\infty} f( k )^* f( k ) e^{ i k \xi } \, dk \\ \displaystyle \qquad = \frac{ 1 }{ 2 \pi } \int^{\infty}_{-\infty} | f( k ) |^2 e^{ i k \xi } \, dk$

つまり、真面目に関数をちょっとずつズラして積分しなくても、フーリエ変換の（強度の）逆フーリエ変換から自己相関関数を求めることが出来る。
今まで、「ふーん」としか思っていなかったが、よく考えると、
$\displaystyle | f( x ) |^2 \neq \frac{ 1 }{ 2 \pi } \int^{\infty}_{-\infty} | f( k ) |^2 e^{ i k x } \, dk$
であり、フーリエ成分を（絶対値の）二乗して逆フーリエしたら全然違う量になっているのは、なかなか面白いのではないか？

この「逆フーリエ変換すると自己相関関数を与える」関数をスペクトル $s(k)$ と呼ぶ。

$\displaystyle s_f( k ) = | f( k ) |^2 \\ \displaystyle h_f( \xi ) = \frac{ 1 }{ 2 \pi } \int^{\infty}_{-\infty} s_f( k ) e^{ i k \xi } \, dk$

特に、 $h( 0 )$ は実関数 $f(x)$ の全強度に対応し、 $h( 0 ) \propto \int s( k ) \, dk$ から、「スペクトル $s(k)$ は（周）波数ごとの強度」と解釈出来ることがわかる。また、計算したスペクトルが正しいかどうか、直接求めた全強度と比較することでチェックすることも出来る。

余談だが、平均値 $\bar{f}$ からのズレである $\delta f(x) = f(x) - \bar{f}$ を扱う方が便利なこともある。
自己相関が分散に対応するように自己相関関数 $H$ を以下のように定義すると、
$\displaystyle H( \xi ) = \frac{ 1 }{ L } \int^b_a \delta f( x ) \, \delta f( x + \xi ) \, dx = \frac{ 1 }{ 2 \pi } \int^{\infty}_{-\infty} S( k ) e^{ i k \xi } \, dk, \\ \displaystyle L = \int^b_a \, dx, \qquad S(k) = \frac{ 1 }{ L } | \delta f( k ) |^2$
この場合、 $H( 0 )$ が全分散を与えるため、スペクトルは（周）波数ごとの分散を与えるものとして解釈出来る。これは揺らぎの解析に利用出来ると考えられる。

自己相関関数があるならば、相互相関関数も定義出来る。
$\displaystyle h_{fg}( \xi ) = \int^b_a f( x ) g( x + \xi ) \, dx = \frac{ 1 }{ 2 \pi } \int^{\infty}_{-\infty} s_{fg}( k ) e^{ i k \xi } \, dk \\ \displaystyle c_{fg}( \xi ) = \frac{ h_{fg}( \xi ) }{ h_f( 0 ) h_g( 0 ) } \\ \displaystyle s_{fg}( k ) = f^*( k ) g( k )$