nano_exit

基礎的なことこそ、簡単な例が必要だと思うのです。

MacにPyQt5をインストール：SIPが入らない。

プログラミング

下記のサイトを参考に、PyQt5をインストールする。
MacとLinuxでPyQtを準備する - Qiita
Qt5.9.2をonline installerでインストール。容量24GBを持って行かれる。MacBook Airには些かキツイが仕様がない。

SIPを入れようとしたところ、"make install"で"Operation not permitted"という文言が出てきてコケる。
調べると、/Systermのdirectoryはsudoでもcp等を受け付けない仕様になっているらしい。
こちらのサイトを参考に解決。
初心者向け MacでOperation not permittedの解決方法 - Qiita

python configure.py --qmake ~/Qt/5.9.2/clang_64/bin/qmake -- sip /System/Library/Frameworks/Python.framework/Version/2.7/bin/sip
"--sip"をつけなかったら、PATHを通すかPATHを指定するか怒られたので、指定することにした。


これで"import PyQt5"でPyQt5のモジュールが呼べるようになった。

スツルム=リウヴィル型微分方程式の表示について

数学

任意の二階の線形微分方程式を次のように書く。

P(x) \frac{ d^2 f(x) }{ d x^2 } + Q(x) \frac{ d f(x) }{ d x } + R(x) f(x) = 0 (1)

物理でよく出て来る微分方程式（例えばシュレーディンガー方程式等）は大体 P(x)が定数で出て来る。
しかし、物理でよく出て来る特殊関数はスツルム＝リウヴィル型の微分方程式の解であり、次の形で表される。

S(x) \frac{ d^2 f(x) }{ d x^2 } + S'(x) \frac{ d f(x) }{ d x } + T(x) f(x) = 0 (2)

ここで S'(x) = \frac{ d S(x) }{ d x }で、見易くするために使った。
この式を変形すると、

\frac{ d }{ d x }( S(x) \frac{ d f(x) }{ d x } ) + T(x) f(x) = 0 (3)

と表せる。
特殊関数が満たす微分方程式の形はこちらの表示でよく記述されることが多い。
これが割と不満だった。物理で自然に出てくる微分方程式に特殊関数解が隠れているかを見たいのに、どう考えてもパッと見てチェックするには不便な表示だと思っていたからである。
しかし(2)の表示にしようとすると、(1)からどうやってS(x)をどう作り出すかで見易さが全然変わってしまう。

とモヤモヤしていたら、(1)から(3)へ一般に変形する方法があった。

P(x) \frac{ d^2 f(x) }{ d x^2 } + Q(x) \frac{ d f(x) }{ d x } + R(x) f(x) = 0
\frac{ d^2 f(x) }{ d x^2 } + \frac{ Q(x) }{ P(x) } \frac{ d f(x) }{ d x } + \frac{ R(x) }{ P(x) } f(x) = 0

ここに任意の関数 S(x)を全体に掛ける。

S(x) \frac{ d^2 f(x) }{ d x^2 } + S(x) \frac{ Q(x) }{ P(x) } \frac{ d f(x) }{ d x } + S(x) \frac{ R(x) }{ P(x) } f(x) = 0

スツルム＝リウヴィル型にするためには、 S(x) \frac{ Q(x) }{ P(x) } = S'(x)が条件となる。
よって、

\frac{ S'(x) }{ S(x) } = \frac{ Q(x) }{ P(x) }
\int dln( S(x) ) = \int dx \frac{ Q(x) }{ P(x) }
S(x) = exp( \int dx \frac{ Q(x) }{ P(x) } )

とS(x)が求まり、 T(x) = S(x) \frac{ R(x) }{ P(x) } と思えば(3)の表記が得られる。
だから(3)の表記でよく微分方程式が書かれているんだなぁと納得した。

追記（2018/11/21）
(3)の形に変換することをLioville変換と呼び、(3)の形によって微分演算が自己随伴であることが明確になる。
http://user.numazu-ct.ac.jp/~hmatsu/senkou0905.pdf
http://hb3.seikyou.ne.jp/home/E-Yama/SturmLiouville.pdf

モンティ・ホール問題とシュテルン=ゲルラッハの実験

数学 量子力学

モンティ・ホール問題
モンティ・ホール問題 - Wikipedia
モンティとはテレビの司会者的な存在らしい。
ルールは以下の通り。

(1) 3つのドア (A, B, C) に（景品、ヤギ、ヤギ）がランダムに入っている。
(2) プレーヤーはドアを1つ選ぶ。
(3) モンティは残りのドアのうち1つを必ず開ける。
(4) モンティの開けるドアは、必ずヤギの入っているドアである。
(5) モンティはプレーヤーにドアを選びなおしてよいと必ず言う。
プレーヤーはドアを選び直すべきか？

wikipediaを見る限り、相当盛り上がった問題だった模様。
実際自分も普通に間違えた。
答えは「選び直すべき」であり、景品の当たる確率は2/3である（選び直さなければ1/3）。

ポイントは「司会者の開ける扉がプレーヤーの選択に依存しているということ」と解釈した。
だから条件付き確率を使わなければ計算出来ない問題となる。
プレーヤーが選択する前に、モンティがヤギの扉を開けるルールだったなら単純に当たる確率は1/2で差はなくなる。

この操作の順序によって確率が変わるのは、量子力学のシュテルン=ゲルラッハの実験の応用問題を彷彿とさせる。

(1)電子の集団からz軸プラス方向のものを抜き出す。この時、電子数は半分になる。
(2)その中から更にx軸プラス方向のものを抜き出す。この時、電子数は半分になる。
(3)その中から更にz軸プラス方向のものを抜き出す。
最後に得られる電子数は元の何分の一か？

量子力学におけるスピンの振舞をキチンと説明しないと理解して貰えないだろうが、答えは1/8になる（はず）。
最初にz軸方向のものを抜き出していたんだから、x軸方向に抜き出した後にまたz軸方向で抜き出しても電子数は変わらない、と思ってしまうかも知れないがそうではない。
スピンの検出では検出の軸を決定すると、それに対してプラスかマイナスかしか検出できない。その間の斜め方向とかは無い。斜め方向に向いていた場合、それは検出軸に対して検出されるプラス・マイナスの数の比で表される。誠に不思議な話であるが、自然がそうなっている。
スピンに対して直交した検出軸を用いた場合には、検出軸に対するプラス・マイナス方向のスピンが半々で出てくる。
つまり、x軸プラス方向に向かせてからz軸プラス成分を抜き出そうとすると、また半分になってしまうのである。

量子力学では操作の順番が重要なケースが多いが、量子力学でなくても人間の直感がなかなか及びにくい領域であることがモンティ・ホール問題で明らかになったと思われる。

分子分母が多項式の関数におけるゼロ近傍の極限

数学 量子力学

そもそも分子分母が多項式の時点でやる気がなくなる。すごくやりたくない。苦手意識が強い。
でも多分それは処方箋が頭に入っていないだけ。
今回は対処法を簡単に考察する。

例えば、球ベッセル関数を球ノイマン関数で割ったものにおける原点近傍の振舞が知りたいとする。
それぞれの関数の原点近傍 \rho \rightarrow 0 での振舞は、

j_l( \rho ) \rightarrow \frac{ \rho^l }{ (2l+1)!! } ( 1 - \frac{ \rho^2 }{ 2(2l+3) } + \cdots )

n_l( \rho ) \rightarrow - \frac{ (2l+1)!! }{ 2l+1 } \frac{ 1 }{ \rho^{ l+1 } } ( 1 + \frac{ \rho^2 }{ 2(2l-1) } + \cdots )

こういう多項式同士を割ったものの式をどうやって解すか？というのが今回の焦点。
どこまで多項式の中身を残すかで近似の精度が変わるが、 \rho \rightarrow 0のよくあるパターンとして「0次の次の項まで残す」ことが挙げられる。
最初にこの手のものに出会った時にまず思ったのは、「 \rho \rightarrow 0なんだから多項式の中身は"1"で良くない？」。
こうしなきゃいけないということは基本的にはないはず。でもその慣習みたいなのがあるから、ここで「なんで？」とつまづくと式のグチャグチャ加減から見通しがかなり悪ってしまうと思う。
個人的には、この「一個上も一応入れとく」というノリは、いわゆる有効数字の扱いに近いと思う。あまり重要でないけれど、切り落とし過ぎると気持ち悪い。どこまで正しいのかハッキリしなくて安心出来ない感じ。
多項式の初項だけ残せばもちろん計算は超楽だけど、例えば、それをさらに別の関数に掛けたりした時に一個上の項が効いてくる場合もある。その精神安定剤として「一個残し」は重要だと思う（もちろんどの次数までの近似にしたいかで話は変わってくるが、そういうことがわかる人は多分特に悩んでいないと思う）。

なので、多項式の中身を \rho^2 まで残すとする。
安直に割ると、

\frac{ j_l( \rho ) }{ n_l( \rho ) } \rightarrow - \frac{ 2l+1 }{ ( (2l+1)!! )^2 } \rho^{2l+1} \frac{ 1 - \frac{ \rho^2 }{ 2(2l+3) } }{ 1 + \frac{ \rho^2 }{ 2(2l-1) } }

ここからどうしようとなるのが、

\frac{ 1 - \frac{ \rho^2 }{ 2(2l+3) } }{ 1 + \frac{ \rho^2 }{ 2(2l-1) } }

である。
部分分数分解を用いて、 1 + \sim としても良いが、結局分母をどうするかという問題は残る。この話は後でまた触れる。
ここで、 \rho \rightarrow 0なので、マクローリン展開 1/(1+x) \sim 1 - x + \dotsで分母を無くす。

( 1 - \frac{ \rho^2 }{ 2(2l+3) } )( 1 - \frac{ \rho^2 }{ 2(2l-1) } ) = 1 - \frac{ \rho^2 }{ 2 } ( \frac{ 1 }{ 2l+3 } + \frac{ 1 }{ 2l-1 } ) + O( \rho^4 ) \sim 1 - \rho^2 \frac{ 2l+1 }{ (2l+3)(2l-1) }

最後のところは O(\rho^4)、つまり[\rho]の4次の項を無視しただけで、式変形自身はいつも通りである。こんな感じで、多項式の中身としては j_l, n_lと同じオーダーで表すことが出来た。

これを部分分数分解を間に挟むとどうなるか？

\frac{ 1 - \frac{ \rho^2 }{ 2(2l+3) } }{ 1 + \frac{ \rho^2 }{ 2(2l-1) } } = 1 + \frac{ - \frac{ \rho^2 }{ 2(2l-1) } - \frac{ \rho^2 }{ 2(2l+3) }}{ 1 + \frac{ \rho^2 }{ 2(2l-1) }} = 1 - \rho^2 \frac{ \frac{ 2l+1 }{ (2l+3)(2l-1) } }{ 1 + \frac{ \rho^2 }{ 2(2l-1) }}

ここでマクローリン展開を使うと同じ解が得られるが、それだったら最初からマクローリン展開を使った方が見通しが良い。問題は、分母に対して 1 + x \rightarrow 1 (x \rightarrow 0)としてしまっても同じ答えになる点である。それを許してしまうと、最初から分母に 1 + x \rightarrow 1の近似をして良いではないか！となり、それによって答えが変わってしまう。
つまり、

\frac{ 1 - \frac{ \rho^2 }{ 2(2l+3) } }{ 1 + \frac{ \rho^2 }{ 2(2l-1) } } \rightarrow 1 - \frac{ \rho^2 }{ 2(2l+3) }

にしてしまうと答えが変わる。
そのため、分母に多項式が来て、かつ無限遠ではない有限の点近傍の振舞が知りたい場合には、テイラー展開によって分母を無くすことを考えた方が無難に思える。

try/except文を用いた欠損データの読み込み

プログラミング

データのフォーマットやらなんやらで、読み込めないデータが混ざっている時、その部分だけをNoneで欠損させて読み込ませたい。
データの区切りが空白" "を場合を想定すると、

f= open( filename, "r" )
lines = f.read().split("\n")
f.close()

for line in lines:

  if not line: continue
  if "\r" in line:
    l = line.strip("\r").split(" ")
  else:
    l = line.split(" ")
  while "" in l: l.remove("")

  data = []
  try:
    data.append( map( float, l ) )
  except:
    ll = []
    for li in l:
      try:
        ll.append( float( li ) )
      except:
        ll.append( None )
    data.append( ll )

最初からmapを使わずに全部のデータを1個ずつfloat出来るかチェックするやり方もあると思うが、何となく泥臭くて嫌だなぁと。
mapで一行丸ごと実数化を試みた後に、上手く行かなかった成分を調べる方が人間に思考に近い気がする。

テイラー展開、パデ近似をpythonで簡単に表せる日が来た

プログラミング 数学

mpmathというモジュールの中にテイラー展開をしてくれmpmath.taylorがいらっしゃる。
Function approximation — mpmath 1.0.0 documentation
mpmath.taylorは展開係数の入ったリストを返してくれる。リストの中身は昇べきの順で並んでいる。

一方、mpmath.polyvalは係数のリストを引数にして多項式の値を返してくれる。
Polynomials — SymPy v0.7.0 documentation
ただし、リストの順番は次数に対して降べきの順である。
したがって、list[::-1]でリストの順番を逆にすればtaylor展開の値がpolyvalですぐに求まる。

#!/usr/bin/env python

import numpy as np
import mpmath as mp
import matplotlib.pyplot as plt

def taylor( f, x, x0, n ):
  coefficients = mp.taylor( f, x0, n)
  return mp.polyval( coefficients[ ::-1], x - x0 )

主要部分はたったこれだけである。
例えばsin関数のマクローリン展開を20乗の項まで展開すると（奇数乗の展開係数はゼロであるため、偶数の次数だけ入力すれば違いを見るのには十分）、

x = np.linspace( 0., 10., 100 )
f = mp.sin
x0 = 0.
for i in range( 10 ):
  plt.plot( x, [ taylor( f, xi, x0, 2 * i ) for xi in x ] ) 
plt.xlim( 0., 10. )
plt.ylim( -5., 5. )
plt.plot( x, [ f( xi ) for xi in x ] )
plt.show()

f:id:koideforest:20171019204501p:plain

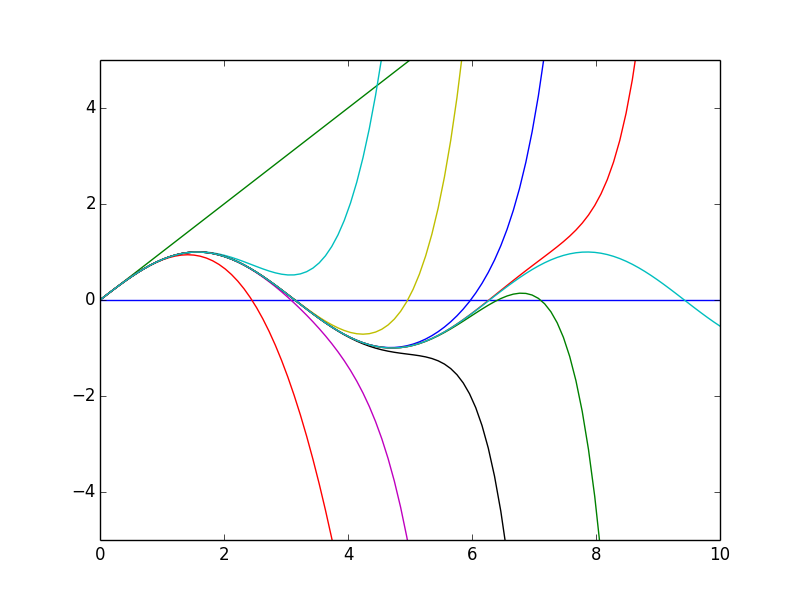
ここでsin関数はmpmathのものでないと動かない。numpy.sinは少なくとも動かなかった。

更に、パデ近似（ペデという人も居るかも）も似たノリで簡単に出来る。
Function approximation — mpmath 1.0.0 documentation
Taylor展開よりも良いと聞かされて来たが、展開係数を求めるのが億劫で、なかなかどんなもんなのか感覚を掴めずにいた。

def pade( f, x, x0, nt, np, nq )
  c_taylor = mp.taylor( f, x0, nt )
  c_p, c_q = mp.pade( c_taylor, np, nq )
  p = mp.polyval( c_p[::-1], x - x0 )
  q = mp.polyval( c_q[::-1], x - x0 )
  return p / q

パデ近似はTaylor展開の次数に合わせて近似を行い、np + nq = ntの制約がかかっている。
とりあえず適当にsin関数を近似してみると、

plt.plot( x, [ taylor( f, xi, x0, 10 ) ], label="taylor" )
plt.plot( x, [ pade( f, xi, x0, 10, 5, 5 ) for xi in x ], label="pade(5,5)" )
plt.plot( x, [ pade( f, xi, x0, 10, 3, 7 ) for xi in x ], label="pade(3,7)" )
plt.plot( x, [ pade( f, xi, x0, 10, 7, 3 ) for xi in x ], label="pade(7,3)" )
plt.plor( x, [ f( xi ) for xi in x ], label="exact" )
plt.legend()
plt.show()

f:id:koideforest:20171019211659p:plain

sin関数だとあまり大きな改善は見られない。
少なくとも、これでいちいち手打ちしなくても近似形が得られるのでだいぶ心がスッキリ。

化学シフト等、メッシュを変えずにグラフをシフト

プログラミング

グラフをただシフトさせるだけだったら、x軸のデータにシフト量を足し引きすればすぐに出来る。
問題は、例えばシフトさせる前と後で差を取りたい場合に、x軸が揃っていないと差が取れない点である。
つまり、横軸のメッシュは固定したまま、グラフだけ並行移動して欲しいのである。

シフトさせるさせないに関わらず、関数系は変えずにx軸だけ変更したい場合には、関数補間が必要になる。
グラフの形を別の関数でなるべく同じになる様に近似することで、データで与えられていない横軸の点でも値を求められるのである。
自分は大抵の場合には3次のスプライン補間（cubic spline）で大丈夫だと（勝手に）思っている。

これをシフトに応用するのだが、一つ問題がある。
補間には有限区間のデータが必要だが、その区間の外側に関しては基本的には補間は扱えない（補間法にも依るのかも知れないが）。それこそ一部を知って全部を知る逆問題みたいな話になってしまうし、そんなものは多くの境界条件を課さない限り（誤差の範囲でも）一意に決まらない。グラフの関数が完全にわかっているなら、全てのx点に対してy点の値が求まっているのと同義なので、そもそもその場合には補間は必要ない。
そして、シフトさせることによってグラフが補間の範囲からはみ出てしまうのである。
以下、手続きを順を追って説明すると、

  1. ( x_i, y_i ) ( i = 1, 2, 3...) のグラフを補間するためのスプライン係数を求める。
  2. これにより、近似関数 f( x ) ( x_{min} \leq x \leq x_{max} )が与えられる。
  3. シフト量を \Deltaとし、 \zeta_i = f( x_i - \Delta )を得る。 \leftarrow
  4. ( x_i, \zeta_i )をプロットすることで、シフトしたグラフを得る。

\zetaを得るところで、 x_i - \Deltaが範囲を飛び出してしまい、(python: scipy.interpolate.interp1dでは)エラーが返って来る。
これを回避するためには、あまり格好は良くないが、 x_i - \Deltaが範囲を飛び出した時には \zeta_i = 0とするのが一番簡単な方法に思える。

tan^{-1}(x)における横軸のシフトをpythonで実装すると、

#!/usr/bin/env python

import numpy as np
import spicy.interpolate as ipl
import matplotlib.pyplot as plt

x = np.linspace( 0, 10, 11 )
y = np.arctan( x )
f = ipl.interp1d( x, y, kind="cubic" )

shift = 2.
x_shift = [ xxx - shift for xxx in x ]

x_min = x[0]
x_max = x[-1]
y_chemshif = []
for xs in x_shift:
  if x_min <= xs <= x_max:
    y_chemshif.append( f( xs ) )
  else:
    y_chemshif.append( 0. )

plt.plot( x, y, "o", color="red" )
plt.plot( x, y_chemshif, "o", color="blue" )
plt.show()

f:id:koideforest:20171019180617p:plain